题目内容
某公司销售A、B、C三款手机,每款手机都有经济型和豪华型两种型号,据统计12月份共销售1000部手机(具体销售情况见下表)
已知在销售1000部手机中,经济型B款手机销售的频率是0.21.
(Ⅰ)现用分层抽样的方法在A、B、C三款手机中抽取50部,求在C款手机中抽取多少部?
(Ⅱ)若y≥136,z≥133,求C款手机中经济型比豪华型多的概率.
| A款手机 | B款手机 | C款手机 | |
| 经济型 | 200 | x | y |
| 豪华型 | 150 | 160 | z |
(Ⅰ)现用分层抽样的方法在A、B、C三款手机中抽取50部,求在C款手机中抽取多少部?
(Ⅱ)若y≥136,z≥133,求C款手机中经济型比豪华型多的概率.
考点:古典概型及其概率计算公式,分层抽样方法
专题:概率与统计
分析:(Ⅰ)由已知,
=0.21,可得x=210.从而求得手机C的总数为280部.根据分层抽样的性质即可得到在C款手机中抽取手机数为14部.
(Ⅱ)设“C款手机中经济型比豪华型多”为事件A,C款手机中经济型、豪华型手机数记为(y,z),满足事件y≥136,z≥133的基本事件有12个,其中事件A包含的基本事件有7个.所以C款手机中经济型比豪华型多的概率为
.
| x |
| 1000 |
(Ⅱ)设“C款手机中经济型比豪华型多”为事件A,C款手机中经济型、豪华型手机数记为(y,z),满足事件y≥136,z≥133的基本事件有12个,其中事件A包含的基本事件有7个.所以C款手机中经济型比豪华型多的概率为
| 7 |
| 12 |
解答:
解:(Ⅰ)∵
=0.21,
∴x=210.
∴手机C的总数为:1000-200-150-210-160=280(部).
现用分层抽样的方法在A、B、C三款手机中抽取50部手机,
应在C款手机中抽取手机数为:14(部).
(Ⅱ)设“C款手机中经济型比豪华型多”为事件A,C款手机中经济型、豪华型手机数记为(y,z),
∵y+z=280,y,z∈N*,
∴满足事件y≥136,z≥133的基本事件有:(136,144),(137,143),(138,142),
(139,141),(140,140),(141,139),(142,138),(143,137),
(144,136),(145,135),(146,134),(147,133)共12个.
事件A包含的基本事件为:(141,139),(142,138),(143,137),(144,136),
(145,135),(146,134),(147,133)共7个
所以P(A)=
.
即C款手机中经济型比豪华型多的概率为
.
| x |
| 1000 |
∴x=210.
∴手机C的总数为:1000-200-150-210-160=280(部).
现用分层抽样的方法在A、B、C三款手机中抽取50部手机,
应在C款手机中抽取手机数为:14(部).
(Ⅱ)设“C款手机中经济型比豪华型多”为事件A,C款手机中经济型、豪华型手机数记为(y,z),
∵y+z=280,y,z∈N*,
∴满足事件y≥136,z≥133的基本事件有:(136,144),(137,143),(138,142),
(139,141),(140,140),(141,139),(142,138),(143,137),
(144,136),(145,135),(146,134),(147,133)共12个.
事件A包含的基本事件为:(141,139),(142,138),(143,137),(144,136),
(145,135),(146,134),(147,133)共7个
所以P(A)=
| 7 |
| 12 |
即C款手机中经济型比豪华型多的概率为
| 7 |
| 12 |
点评:本题考查分层抽样,古典概型及概率计算等知识的综合应用,属于中档题.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
“函数y=sin(x+φ)为偶函数”是“φ=
”的( )
| π |
| 2 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
在平面直角坐标系中,x轴的正半轴上有4个点,y轴的正半轴上有5个点,这9个点任意两点连线,则所有连线段的交点落入第一象限的个数最多是( )
| A、30 | B、60 |
| C、120 | D、240 |

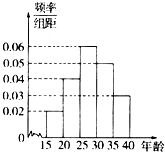 山东省第二十三届运动会将于2014年9月16日在济宁市开幕,为办好省运会,济宁市计划招募各类志愿者1.2万人.为做好宣传工作,招募小组对济宁市15-40岁的人群随机抽取了100人,回答“省运会”的有关知识,根据统计结果制作了如下的统计图及表:
山东省第二十三届运动会将于2014年9月16日在济宁市开幕,为办好省运会,济宁市计划招募各类志愿者1.2万人.为做好宣传工作,招募小组对济宁市15-40岁的人群随机抽取了100人,回答“省运会”的有关知识,根据统计结果制作了如下的统计图及表: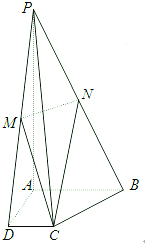 如图,四棱锥P-ABCD,PA⊥平面ABCD,且PA=4,底面ABCD为直角梯形,∠CDA=∠BAD=90°,AB=2,CD=1,
如图,四棱锥P-ABCD,PA⊥平面ABCD,且PA=4,底面ABCD为直角梯形,∠CDA=∠BAD=90°,AB=2,CD=1,
 在三棱锥S-ABC中,∠SAB=∠SAC=∠ACB=90°,
在三棱锥S-ABC中,∠SAB=∠SAC=∠ACB=90°,