题目内容
已知定义域为（-∞，0）∪（0，+∞）的偶函数f（x）在（0，+∞）上为增函数，且f（1）=0，则不等式f（x）＞0的解集为 ．
考点：奇偶性与单调性的综合
专题：函数的性质及应用
分析：根据偶函数与函数单调性之间的关系即可得到结论．
解答：
解：∵偶函数f（x）在（0，+∞）上为增函数，且f（1）=0，
∴不等式f（x）＞0等价为f（x）＞f（1），即f（|x|）＞f（1），
则|x|＞1，解得x＞1或x＜-1，
故答案为：（-∞，-1）∪（1，+∞）
∴不等式f（x）＞0等价为f（x）＞f（1），即f（|x|）＞f（1），
则|x|＞1，解得x＞1或x＜-1，
故答案为：（-∞，-1）∪（1，+∞）
点评：本题主要考查不等式的求解，根据函数奇偶性和单调性之间的关系将不等式进行转化是解决本题的关键．
练习册系列答案
相关题目
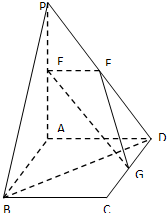如图，平面PAD⊥平面ABCD，ABCD为正方形，∠PAD=90°，且PA=AD=2，E，F，G分别是线段PA、PD、CD的中点．