题目内容
a为正数，记[a]表示取a的整数部分，已知a-[a]、[a]、a，依次成等比数列，则a= ．
考点：等比数列的性质
专题：计算题,等差数列与等比数列
分析：由题意，整数部分x≥0，小数部分y属于[0，1）y，x，x+y成等比数列，所以x＞0，求出x，y，即可得出结论．
解答：
解：由题意，整数部分x≥0，小数部分y属于[0，1）
y，x，x+y成等比数列，所以x＞0
x2=y（x+y）=＞x2-xy-y2=0
因为x＞0，所以x=
y，
因为0≤y＜1
所以0≤x＜
，对应正整数x，只能取1
所以x=1，y2+y-1=0
从而y=
，因此a=x+y=
．
故答案为：
．
y，x，x+y成等比数列，所以x＞0
x2=y（x+y）=＞x2-xy-y2=0
因为x＞0，所以x=
1+
| ||
| 2 |
因为0≤y＜1
所以0≤x＜
1+
| ||
| 2 |
所以x=1，y2+y-1=0
从而y=
-1+
| ||
| 2 |
1+
| ||
| 2 |
故答案为：
1+
| ||
| 2 |
点评：本题考查等比数列的性质，考查学生的计算能力，比较基础．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知点A（-2，0），点B（2，0），若kMA•kMB=-1，则动点M的轨迹方程为（ ）
| A、x2-y2=4（x≠±2） |
| B、x2-y2=4 |
| C、x2+y2=4（x≠±2） |
| D、x2+y2=4 |
复数
在复平面上对应的点位于（ ）
| i |
| 3-i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
下列函数为幂函数的是（ ）
①y=x2+1； ②y=2x； ③y=
； ④y=（x-1）2； ⑤y=x5； ⑥y=xx+1．
①y=x2+1； ②y=2x； ③y=
| 1 |
| x2 |
| A、①③⑤ | B、①②⑤ |
| C、③⑤ | D、④⑤⑥ |
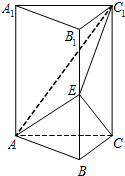如图，直三棱柱ABC-A1B1C1中，∠ABC=90°，AB=BC=1，CC1=