题目内容
设Sn为等差数列{an}的前n项和,已知S3=a7,a8-2a3=3.
(1)求an;
(2)设bn=
,数列{bn}的前n项和记为Tn,求Tn.
(1)求an;
(2)设bn=
| 1 |
| Sn |
考点:数列的求和,等差数列的性质
专题:等差数列与等比数列
分析:(1)由题意联立方程组解得首项及公差即得;
(2)利用裂项相消法求和即可得出结论.
(2)利用裂项相消法求和即可得出结论.
解答:
解:(1)设数列{an}的公差为d,由题得
,(3分)
解得a1=3,d=2,(5分)
∴an=a1+(n-1)d=2n+1; (6分)
(2)由(1)得,Sn=na1+
•d=n(n+2),(8分)
∴bn=
=
(
-
),(10分)
∴Tn=b1+b2+…+bn=
[(1-
)+(
-
)+…+(
-
)+(
-
)]
=
(1+
-
-
)
=
+
.(12分)
|
解得a1=3,d=2,(5分)
∴an=a1+(n-1)d=2n+1; (6分)
(2)由(1)得,Sn=na1+
| n(n-1) |
| 2 |
∴bn=
| 1 |
| n(n+2) |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+2 |
∴Tn=b1+b2+…+bn=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| n-1 |
| 1 |
| n+1 |
| 1 |
| n |
| 1 |
| n+2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| n+1 |
| 1 |
| n+2 |
=
| 3 |
| 4 |
| 2n+3 |
| 2(n+1)(n+2) |
点评:本题考查等差数列的性质、数列的基本运算及利用裂项相消法求数列和的知识,考查学生的运算能力及方程思想的运用能力,属中档题.

练习册系列答案
相关题目
 定义在R上的函数f(x)满足f(4)=1,已知f(x)的导函数f(x)′的图象如图所示,若两个正数a、b满足f(2a+b)<1,则
定义在R上的函数f(x)满足f(4)=1,已知f(x)的导函数f(x)′的图象如图所示,若两个正数a、b满足f(2a+b)<1,则| a+2b+3 |
| a+1 |
A、(
| ||||
B、(-∞,
| ||||
C、(
| ||||
| D、(-∞,3) |
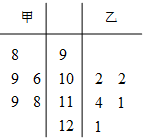 在数学趣味知识培训活动中,甲、乙两名学生的5次培训成绩如图茎叶图所示:
在数学趣味知识培训活动中,甲、乙两名学生的5次培训成绩如图茎叶图所示: