题目内容
在△ABC中,角A,B,C所对的边分别是a,b,c且sinB+cosB=1-sin
.
(Ⅰ)求cosB的值;
(Ⅱ)若a+c=4,求△ABC的面积的最大值.
| B |
| 2 |
(Ⅰ)求cosB的值;
(Ⅱ)若a+c=4,求△ABC的面积的最大值.
考点:二倍角的余弦,二倍角的正弦
专题:解三角形
分析:(Ⅰ)在△ABC中,由条件利用二倍角公式可得 cos
-sin
=-
<0 ①,
∈(
,
).再把①平方求得sinB的值,即可得到cosB的值.
(Ⅱ)由a+c=4,△ABC的面积S=
ac•sinB=
ac,里哦也难怪基本不等式求得S的最大值.
| B |
| 2 |
| B |
| 2 |
| 1 |
| 2 |
| B |
| 2 |
| π |
| 4 |
| π |
| 2 |
(Ⅱ)由a+c=4,△ABC的面积S=
| 1 |
| 2 |
| 3 |
| 8 |
解答:
解:(Ⅰ)在△ABC中,∵sinB+cosB=1-sin
,
∴2sin
cos
-2sin2
+sin
=0,
∴cos
-sin
=-
<0 ①,∴
∈(
,
).
再把①平方可得 2sin
cos
=
,
∴sinB=
,∴cosB=-
.
(Ⅱ)∵a+c=4,
∴△ABC的面积S=
ac•sinB=
ac≤
×(
)2=
,
当且仅当a=c=2时,取等号,故△ABC的面积S的最大值为
.
| B |
| 2 |
∴2sin
| B |
| 2 |
| B |
| 2 |
| B |
| 2 |
| B |
| 2 |
∴cos
| B |
| 2 |
| B |
| 2 |
| 1 |
| 2 |
| B |
| 2 |
| π |
| 4 |
| π |
| 2 |
再把①平方可得 2sin
| B |
| 2 |
| B |
| 2 |
| 3 |
| 4 |
∴sinB=
| 3 |
| 4 |
| ||
| 4 |
(Ⅱ)∵a+c=4,
∴△ABC的面积S=
| 1 |
| 2 |
| 3 |
| 8 |
| 3 |
| 8 |
| a+c |
| 2 |
| 3 |
| 2 |
当且仅当a=c=2时,取等号,故△ABC的面积S的最大值为
| 3 |
| 2 |
点评:本题主要考查二倍角的三角公式、同角三角函数的基本关系,基本不等式的应用,属于中档题.

练习册系列答案
相关题目
下列函数中,既是偶函数且值域为(-∞,0]的函数是( )
| A、f(x)=xsinx |
| B、f(x)=-2-x |
| C、f(x)=ln|x| |
| D、f(x)=-x2 |
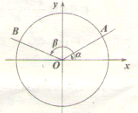 如图所示,锐角α和钝角β的始边与x轴的非负半轴重合,终边分别与单位圆交于A、B两点,角α的终边与射线y=
如图所示,锐角α和钝角β的始边与x轴的非负半轴重合,终边分别与单位圆交于A、B两点,角α的终边与射线y=