题目内容
以直角坐标系的原点为极点,x轴的正半轴为极轴,并在两种坐标系中取相同的长度单位已知直线的极坐标方程为θ=
(ρ∈R),它与曲线
(θ为参数)相交于两点A和B,求|AB|.
| π |
| 4 |
|
考点:参数方程化成普通方程
专题:选作题,坐标系和参数方程
分析:把参数方程、极坐标方程化为直角坐标方程,求出弦心距,再利用弦长公式求得弦长|AB|的值.
解答:
解:直线的极坐标方程为θ=
(ρ∈R),化为直角坐标方程为x-y=0.
曲线
(θ为参数)的普通方程为 (x-2)2+(y-1)2=5,表示以(2,1)为圆心,半径R等于
的圆,…(2分)
从而C到直线y=x的距离d=
…(3分)
由垂径定理得,|AB|=2
=3
…(4分)
| π |
| 4 |
曲线
|
| 5 |
从而C到直线y=x的距离d=
| ||
| 2 |
由垂径定理得,|AB|=2
| R2-d2 |
| 2 |
点评:本题主要考查把参数方程、极坐标方程化为直角坐标方程的方法,直线和圆的位置关系,点到直线的距离公式,弦长公式的应用,属于基础题.

练习册系列答案
相关题目
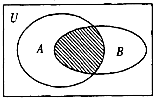
设全集U=R,A={x|
<0},B={x|x<-1},则如图中阴影部分表示的集合为( )
| x |
| x+3 |

| A、{x|x>0} |
| B、{x|-3<x<-1} |
| C、{x|-3<x<0} |
| D、{x|x<-1} |
已知{an}为等比数列,公比为q,若a2•a3=2a1,且a4与2a7的等差中项为
,则q=( )
| 5 |
| 4 |
A、
| ||
B、
| ||
| C、2 | ||
| D、4 |
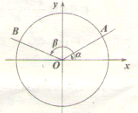 如图所示,锐角α和钝角β的始边与x轴的非负半轴重合,终边分别与单位圆交于A、B两点,角α的终边与射线y=
如图所示,锐角α和钝角β的始边与x轴的非负半轴重合,终边分别与单位圆交于A、B两点,角α的终边与射线y= 如图是某中学甲、乙两名学生2014年篮球比赛每场比赛得分的茎叶图,则甲、乙两名学生得分的中位数之和是
如图是某中学甲、乙两名学生2014年篮球比赛每场比赛得分的茎叶图,则甲、乙两名学生得分的中位数之和是