题目内容
定义在R上的函数f（x）满足f（4）=1，已知f（x）的导函数f（x）′的图象如图所示，若两个正数a、b满足f（2a+b）＜1，则| a+2b+3 |
| a+1 |
A、（
| ||||
B、（-∞，
| ||||
C、（
| ||||
| D、（-∞，3） |
考点：利用导数研究函数的单调性
专题：数形结合法
分析：由已知导函数的图象，判断出函数f（x）在（0，+∞）上单调递增，结合已知条件，得出a，b满足的条件，画出可行域，而
变形后，表示的是斜率．
| a+2b+3 |
| a+1 |
解答：
解：由f（x）′的图象知，f（x）在（-∞，0）上单调递减，在（0，+∞）上单调递增，
又∵f（2a+b）＜1且f（4）=1⇒2a+b＜4，
∴a，b 满足
画出可行域△0AB内部，如图所示：
=1+2×
，∵
表示可行域△OAB内部的点与点P（-1，-1）的斜率，
∴KPA＜
＜KPB，又KPA=
=
，KPB=
=5，
∴
＜1+2×
＜11．
故选：C．
解：由f（x）′的图象知，f（x）在（-∞，0）上单调递减，在（0，+∞）上单调递增，又∵f（2a+b）＜1且f（4）=1⇒2a+b＜4，
∴a，b 满足
|
| a+2b+3 |
| a+1 |
| b+1 |
| a+1 |
| b+1 |
| a+1 |
∴KPA＜
| b+1 |
| a+1 |
| 0+1 |
| 2+1 |
| 1 |
| 3 |
| 4+1 |
| 0+1 |
∴
| 5 |
| 3 |
| b+1 |
| a+1 |
故选：C．
点评：本题考查的了，函数的单调性，线性规划，数形结合．属于常规题，中等难度．
练习册系列答案
相关题目
设A是整数集的一个非空子集，对于k∈A，如果k-1∉A且k+1∉A，那么称k是A的一个“孤立元”，给定S={1，2，3，4，5，6，7，8}，则S的3个元素构成的所有集合中，其元素都是“孤立元”的集合个数是（ ）
| A、6 | B、15 | C、20 | D、25 |
设全集U=R，A={x|
＜0}，B={x|x＜-1}，则如图中阴影部分表示的集合为（ ）
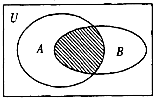
| x |
| x+3 |
| A、{x|x＞0} |
| B、{x|-3＜x＜-1} |
| C、{x|-3＜x＜0} |
| D、{x|x＜-1} |
一个算法的程序框图如图所示，若该程序输出的结果为12，则判断框中应填入的条件是（ ）| A、k≤4 | B、k≤3 |
| C、k＜3 | D、k≥3 |
P为函数y=ex图象上的点，则点P到直线y=x的最短距离为（ ）
| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
下列函数中，既是偶函数且值域为（-∞，0]的函数是（ ）
| A、f（x）=xsinx |
| B、f（x）=-2-x |
| C、f（x）=ln|x| |
| D、f（x）=-x2 |
已知{an}为等比数列，公比为q，若a2•a3=2a1，且a4与2a7的等差中项为
，则q=（ ）
| 5 |
| 4 |
A、
| ||
B、
| ||
| C、2 | ||
| D、4 |