题目内容
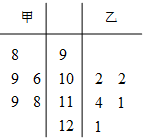 在数学趣味知识培训活动中,甲、乙两名学生的5次培训成绩如图茎叶图所示:
在数学趣味知识培训活动中,甲、乙两名学生的5次培训成绩如图茎叶图所示:(Ⅰ)从甲、乙两人中选择1人参加数学趣味知识竞赛,你会选哪位?请运用统计学的知识说明理由;
(Ⅱ)从乙的5次培训成绩中随机选择2个,试求选到121分的概率.
考点:古典概型及其概率计算公式,茎叶图,众数、中位数、平均数,极差、方差与标准差
专题:概率与统计
分析:第(1)问应先比较两人的平均值,派均值大的去参加竞赛,若均值相等,则再计算方差,选择方差小的去;
第(2)问是一个古典概型问题,应先列举,再利用公式计算.
第(2)问是一个古典概型问题,应先列举,再利用公式计算.
解答:
解:(Ⅰ)甲、乙两人的平均成绩分别是
甲=
=110,
乙=
=110.
甲、乙两人成绩的方差分别是
=
[(98-110)2+(106-110)2+(109-110)2+(118-110)2+(119-110)2]=
,
=
[(102-110)2+(102-110)2+(111-110)2+(114-110)2+(121-110)2]=
由
甲=
乙,
>
,可知甲和乙成绩的平均水平一样,乙的方差小,乙发挥比甲稳定,故选择乙.
(Ⅱ)从乙的5次培训成绩中随机选择2个,共有10个基本事件,分别是:
{111,114},{111,121},{114,121},{102,102},{102,111},{102,114},{102,121},{102,111},{102,114},{102,121},
其中选到121分的基本事件有4个,故选到121分的概率是p=
=
.
. |
| x |
| 98+106+109+118+119 |
| 5 |
. |
| x |
| 102+102+111+114+121 |
| 5 |
甲、乙两人成绩的方差分别是
| s | 2 甲 |
| 1 |
| 5 |
| 306 |
| 5 |
| s | 2 乙 |
| 1 |
| 5 |
| 266 |
| 5 |
由
. |
| x |
. |
| x |
| s | 2 甲 |
| s | 2 乙 |
(Ⅱ)从乙的5次培训成绩中随机选择2个,共有10个基本事件,分别是:
{111,114},{111,121},{114,121},{102,102},{102,111},{102,114},{102,121},{102,111},{102,114},{102,121},
其中选到121分的基本事件有4个,故选到121分的概率是p=
| 4 |
| 10 |
| 2 |
| 5 |
点评:此题属于容易题,考查了茎叶图的视图、均值、方差计算及应用;古典概型的计算问题.

练习册系列答案
相关题目
 一个算法的程序框图如图所示,若该程序输出的结果为12,则判断框中应填入的条件是( )
一个算法的程序框图如图所示,若该程序输出的结果为12,则判断框中应填入的条件是( )| A、k≤4 | B、k≤3 |
| C、k<3 | D、k≥3 |
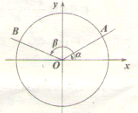 如图所示,锐角α和钝角β的始边与x轴的非负半轴重合,终边分别与单位圆交于A、B两点,角α的终边与射线y=
如图所示,锐角α和钝角β的始边与x轴的非负半轴重合,终边分别与单位圆交于A、B两点,角α的终边与射线y=