题目内容
已知动圆M与⊙O1:x2+(y-1)2=1和⊙O2:x2+(y+1)2=4都外切,求动圆圆心M的轨迹方程.
考点:轨迹方程
专题:计算题,圆锥曲线的定义、性质与方程
分析:设动圆的半径为r,然后根据动圆M与⊙O1:x2+(y-1)2=1和⊙O2:x2+(y+1)2=4都外切,得|MO2|=2+r,|MO1|=1+r,两式相减消去参数r,则满足双曲线的定义,问题解决.
解答:
解:设动圆的半径为r,
而圆x2+(y-1)2=1的圆心为O1(0,1),半径为1;
圆x2+(y+1)2=4的圆心为O2(0,-1),半径为2.
依题意得|MO2|=2+r,|MO1|=1+r,
则|MO2|-|MO1|=(2+r)-(1+r)=1<|O1O2|,
所以点M的轨迹是以O1、O2为焦点的双曲线的上支,且2a=1,c=1,
∴a=
,b=
,
∴动圆圆心M的轨迹方程是
-
=1(y≥
).
而圆x2+(y-1)2=1的圆心为O1(0,1),半径为1;
圆x2+(y+1)2=4的圆心为O2(0,-1),半径为2.
依题意得|MO2|=2+r,|MO1|=1+r,
则|MO2|-|MO1|=(2+r)-(1+r)=1<|O1O2|,
所以点M的轨迹是以O1、O2为焦点的双曲线的上支,且2a=1,c=1,
∴a=
| 1 |
| 2 |
| ||
| 2 |
∴动圆圆心M的轨迹方程是
| y2 | ||
|
| x2 | ||
|
| 1 |
| 2 |
点评:本题以两圆的位置关系为载体,考查双曲线的定义,考查轨迹方程,确定轨迹是双曲线是关键.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
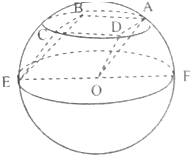 如图,三棱柱OAD-EBC,其中A,B,C,D,E均在以O为球心,半径为2的球面上,EF为直径,侧面ABCD为边长等于2的正方形,则三棱柱OAD-EBC的体积为( )
如图,三棱柱OAD-EBC,其中A,B,C,D,E均在以O为球心,半径为2的球面上,EF为直径,侧面ABCD为边长等于2的正方形,则三棱柱OAD-EBC的体积为( )A、4
| ||
B、4
| ||
C、2
| ||
D、2
|