题目内容
设等差数列{an}的前n项和为Sn,若S13=78,a7+a12=10,则a17= .
考点:等差数列的前n项和
专题:等差数列与等比数列
分析:由等差数列的通项公式与前n项和公式,求出首项a1与公差d,即可求出a17来.
解答:
解:在等差数列{an}中,
∵S13=78,a7+a12=10,
∴
,
解得
;
∴a17=a1+16d=
-
=2.
故答案为:2.
∵S13=78,a7+a12=10,
∴
|
解得
|
∴a17=a1+16d=
| 42 |
| 5 |
| 32 |
| 5 |
故答案为:2.
点评:本题考查了等差数列的通项公式与前n项和公式的应用问题,解题时应根据题意,合理地利用等差数列的通项公式与前n项和公式,进行解答即可,是基础题.

练习册系列答案
相关题目
已知直线mx+(1-n)y+1=0(m>0,n>0)和直线x+2y+1=0平行,则
+
的最小值是( )
| 1 |
| m |
| 1 |
| n |
A、2
| ||
B、3+2
| ||
C、4
| ||
D、3+
|
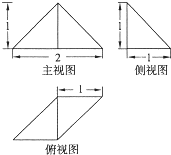
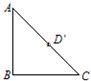 将一个边长为2的正方形ABCD沿其对角线AC折起,其俯视图如图所示,此时连接顶点B,D形成三棱锥B-ACD,则其正(主)视图的面积为( )
将一个边长为2的正方形ABCD沿其对角线AC折起,其俯视图如图所示,此时连接顶点B,D形成三棱锥B-ACD,则其正(主)视图的面积为( )