题目内容
给出如下四个命题:
①若“p∨q”为真命题,则p、q均为真命题;
②“若a>b,则2a>2b-1”的否命题为“若a≤b,则2a≤2b-1”;
③“?x∈R,x2+x≥1”的否定是“?x0∈R,x02+x0≤1”;
④“x>0”是“x+
≥2”的充要条件.
其中不正确的命题是( )
①若“p∨q”为真命题,则p、q均为真命题;
②“若a>b,则2a>2b-1”的否命题为“若a≤b,则2a≤2b-1”;
③“?x∈R,x2+x≥1”的否定是“?x0∈R,x02+x0≤1”;
④“x>0”是“x+
| 1 |
| x |
其中不正确的命题是( )
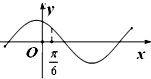
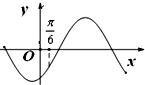
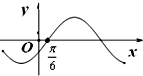
| A、①② | B、②③ | C、①③ | D、③④ |
考点:命题的真假判断与应用
专题:综合题,简易逻辑
分析:①“p∨q”为真命题,p、q二者中只要有一真即可;
②写出一个命题的否命题的关键是正确找出原命题的条件和结论;
③直接写出全称命题的否定判断;
④利用基本不等式,可得结论.
②写出一个命题的否命题的关键是正确找出原命题的条件和结论;
③直接写出全称命题的否定判断;
④利用基本不等式,可得结论.
解答:
解:①“p∨q”为真命题,p、q二者中只要有一真即可,故不正确;
②“若a>b,则2a>2b-1”的否命题为“若a≤b,则2a≤2b-1”,正确;
③“?x∈R,x2+x≥1”的否定是“?x0∈R,x02+x0<1”,故不正确;
④“x>0”时,“x+
≥2”,若“x+
≥2”,则“x>0”,∴“x>0”是“x+
≥2”的充要条件,故正确.
故选:C.
②“若a>b,则2a>2b-1”的否命题为“若a≤b,则2a≤2b-1”,正确;
③“?x∈R,x2+x≥1”的否定是“?x0∈R,x02+x0<1”,故不正确;
④“x>0”时,“x+
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
故选:C.
点评:本题考查命题的真假判断与应用,考查复合命题的真假判断,考查了命题的否命题、全称命题的否定、充要条件,属于中档题.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
设正弦函数f(x)=cosx在x=0和x=
处得切线得斜率分别为k1,k2,则k1,k2的大小关系为( )
| π |
| 2 |
| A、k1<k2 |
| B、k1>k2 |
| C、k1=k2 |
| D、不确定 |
已知两不重合直线a、b及两不重合平面α、β,那么下列命题中正确的是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
已知圆x2-x+y2=6经过双曲线
-
=1(a,b>0)的左顶点和右焦点,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
| B、2 | ||||
C、
| ||||
D、
|
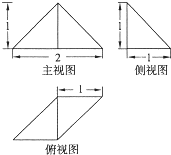
 将一个边长为2的正方形ABCD沿其对角线AC折起,其俯视图如图所示,此时连接顶点B,D形成三棱锥B-ACD,则其正(主)视图的面积为( )
将一个边长为2的正方形ABCD沿其对角线AC折起,其俯视图如图所示,此时连接顶点B,D形成三棱锥B-ACD,则其正(主)视图的面积为( )