题目内容
已知函数f(x)=1+x-
+
-
+…+
,g(x)=1-x+
-
+
-…-
.设 F(x)=f(x+4).g(x-4),且函数F(x)的零点在区间[a-1,a]或[b-1,b](a<b,a,b∈Z)内,则a+b的值为( )
| x2 |
| 2 |
| x3 |
| 3 |
| x4 |
| 4 |
| x2013 |
| 2013 |
| x2 |
| 2 |
| x3 |
| 3 |
| x4 |
| 4 |
| x2013 |
| 2013 |
| A、-1 | B、0 | C、1 | D、2 |
考点:函数的零点,二项式定理的应用
专题:函数的性质及应用
分析:可通过导数法求得f(x)与g(x)的零点,从而可得f(x+4)和g(x-4)的零点,继而函数F(x)的零点在区间[a-1,a]或[b-1,b](a<b,a,b∈Z)内,求得a,b的值.
解答:
解:∵f′(x)=1-x+x2+…+x2012,
①x=0时,f′(0)=1>0;
②当x=-1时,f′(-1)=2013>0;
③当x≠0,-1时,f′(x)=
=
,无论x>-1,还是x<-1,都有f′(x)>0.
综上可知:对任意x∈R,都有f′(x)>0.
∴函数f(x)单调递增,也就是说,函数f(x)至多有一个零点.
由函数零点的判定定理可知:函数f(x)的零点x0∈(-1,0).
由-1<x+4<0得:-5<x<-4,
∴f(x+4)在[-5,-4]有唯一零点.
又g(x)=1-x+
-
+
-…-
.
∴g′(x)=(-1+x)+(-x2+x3)+…-x2012
=-[(1-x)+(x2-x3)+…+x2012]
=-f′(x)<0,
∴g(x)在R上单调递减;
又g(1)>0,g(2)<0,
∴g(x)在(1,2)上有唯一零点,
由1<x-4<2得:5<x<6,
∴g(x-4)在[5,6]上有唯一零点.
∵F(x)=f(x+4).g(x-4),且函数F(x)的零点在区间[a-1,a]或[b-1,b](a<b,a,b∈Z)内
∴F(x)的零点即为f(x+4)和g(x-4)的零点.
∴a=-4,b=6,
即a+b=2.
故选:D.
①x=0时,f′(0)=1>0;
②当x=-1时,f′(-1)=2013>0;
③当x≠0,-1时,f′(x)=
| 1-(-x)2013 |
| 1-(-x) |
| 1+x2013 |
| 1+x |
综上可知:对任意x∈R,都有f′(x)>0.
∴函数f(x)单调递增,也就是说,函数f(x)至多有一个零点.
由函数零点的判定定理可知:函数f(x)的零点x0∈(-1,0).
由-1<x+4<0得:-5<x<-4,
∴f(x+4)在[-5,-4]有唯一零点.
又g(x)=1-x+
| x2 |
| 2 |
| x3 |
| 3 |
| x4 |
| 4 |
| x2013 |
| 2013 |
∴g′(x)=(-1+x)+(-x2+x3)+…-x2012
=-[(1-x)+(x2-x3)+…+x2012]
=-f′(x)<0,
∴g(x)在R上单调递减;
又g(1)>0,g(2)<0,
∴g(x)在(1,2)上有唯一零点,
由1<x-4<2得:5<x<6,
∴g(x-4)在[5,6]上有唯一零点.
∵F(x)=f(x+4).g(x-4),且函数F(x)的零点在区间[a-1,a]或[b-1,b](a<b,a,b∈Z)内
∴F(x)的零点即为f(x+4)和g(x-4)的零点.
∴a=-4,b=6,
即a+b=2.
故选:D.
点评:本题考查函数的零点,考查利用导数判断函数的单调性及零点存在定理的应用,考查综合分析与转化的能力,属于难题.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
已知两不重合直线a、b及两不重合平面α、β,那么下列命题中正确的是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
二次不等式ax2+bx+1>0的解集为{x|-1<x<
},则ab的值为( )
| 1 |
| 3 |
| A、-5 | B、5 | C、-6 | D、6 |
已知圆x2-x+y2=6经过双曲线
-
=1(a,b>0)的左顶点和右焦点,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
| B、2 | ||||
C、
| ||||
D、
|
已知直线mx+(1-n)y+1=0(m>0,n>0)和直线x+2y+1=0平行,则
+
的最小值是( )
| 1 |
| m |
| 1 |
| n |
A、2
| ||
B、3+2
| ||
C、4
| ||
D、3+
|
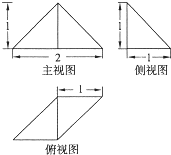
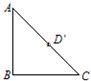 将一个边长为2的正方形ABCD沿其对角线AC折起,其俯视图如图所示,此时连接顶点B,D形成三棱锥B-ACD,则其正(主)视图的面积为( )
将一个边长为2的正方形ABCD沿其对角线AC折起,其俯视图如图所示,此时连接顶点B,D形成三棱锥B-ACD,则其正(主)视图的面积为( )