题目内容
已知双曲线
-
=1(a>0,b>0)的左焦点为F,若该双曲线上存在点P,满足以双曲线虚轴为直径的圆与线段PF相切与线段PF的中点,则该双曲线的离心率为 .
| x2 |
| a2 |
| y2 |
| b2 |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:设PF的中点为M,双曲线的右焦点为F′(c,0),连结OM、PF′(O为坐标原点),则|PF′|=2|OM|=2b且PF⊥PF′,可得PF,利用勾股定理,求出b=2a,即可求出双曲线的离心率.
解答:
解:由题意可知点P在双曲线的左支上且b>a,
设PF的中点为M,双曲线的右焦点为F′(c,0),连结OM、PF′(O为坐标原点),
则|PF′|=2|OM|=2b且PF⊥PF′,
∴PF=PF′-2a=2b-2a,|PF|2+|PF′|2=|FF′|2,即(2b-2a)2+(2b)2=(2c)2,得b=2a,
则该双曲线的离心率e=
=
.
故答案为:
.
设PF的中点为M,双曲线的右焦点为F′(c,0),连结OM、PF′(O为坐标原点),
则|PF′|=2|OM|=2b且PF⊥PF′,
∴PF=PF′-2a=2b-2a,|PF|2+|PF′|2=|FF′|2,即(2b-2a)2+(2b)2=(2c)2,得b=2a,
则该双曲线的离心率e=
| ||
| a |
| 5 |
故答案为:
| 5 |
点评:本题考查双曲线的离心率,考查双曲线的定义,考查学生的计算能力,属于基础题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
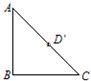 将一个边长为2的正方形ABCD沿其对角线AC折起,其俯视图如图所示,此时连接顶点B,D形成三棱锥B-ACD,则其正(主)视图的面积为( )
将一个边长为2的正方形ABCD沿其对角线AC折起,其俯视图如图所示,此时连接顶点B,D形成三棱锥B-ACD,则其正(主)视图的面积为( )