题目内容
已知点A(1,0),若曲线Γ上存在四个点B,C,D,E,使得△ABC和△ADE都是正三角形,则称曲线Γ为“黄金曲线”,给定下列四条曲线:①4x+3y2=0;②x2+y2=
;③
+y2=1;④
-y2=1.其中,“黄金曲线”的个数是( )
| 1 |
| 4 |
| x2 |
| 2 |
| x2 |
| 3 |
| A、1 | B、2 | C、3 | D、4 |
考点:命题的真假判断与应用
专题:新定义,圆锥曲线的定义、性质与方程
分析:四条曲线都关于x轴对称,过点A(1,0)作倾斜角分别为30°,150°的直线l1,l2,根据图象,结合新定义,即可得出结论.
解答:
解:4条曲线都关于x轴对称,过点A(1,0)分别作倾斜角分别为30°,150°的直线l1,l2,
如图可得,只有曲线3上存在四个点B,C,D,E,使△ABC与△ADE都是正三角形,
故选:A.
如图可得,只有曲线3上存在四个点B,C,D,E,使△ABC与△ADE都是正三角形,

故选:A.
点评:本题是新定义问题,解题的关键是读懂题目的意思,正确运用新定义.

练习册系列答案
相关题目
二次不等式ax2+bx+1>0的解集为{x|-1<x<
},则ab的值为( )
| 1 |
| 3 |
| A、-5 | B、5 | C、-6 | D、6 |
函数f(x)=xsinx在区间[0,4]上的零点个数( )
| A、0 | B、1 | C、2 | D、3 |
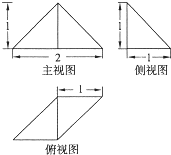
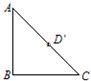 将一个边长为2的正方形ABCD沿其对角线AC折起,其俯视图如图所示,此时连接顶点B,D形成三棱锥B-ACD,则其正(主)视图的面积为( )
将一个边长为2的正方形ABCD沿其对角线AC折起,其俯视图如图所示,此时连接顶点B,D形成三棱锥B-ACD,则其正(主)视图的面积为( )