��Ŀ����
��֪����f(x)=mx3+nx2(m��n��R ,m��0)��ͼ���ڣ�2��f(2)������������x��ƽ��.
��1����n��m�Ĺ�ϵʽ����f(x)�ĵ��������䣻
��2��֤����������ʵ��0<x1<x2<1, ����x�ķ��̣�
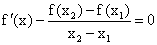 �ڣ�x1,x2������ʵ����
�ڣ�x1,x2������ʵ����
��3����ϣ�2���Ľ��ۣ���ʵ����������������ֵ������������f(x)���ڱ�����[a,b]���������ϵĺ�������������(a,b)�ڵ��������ڣ�����(a,b)�����ٴ���һ��x0��ʹ��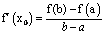 .��������ѧ����ָ�������������������Һ����ȶ���������������ֵ��������.��������������ֵ����֤����
.��������ѧ����ָ�������������������Һ����ȶ���������������ֵ��������.��������������ֵ����֤����
��0<a<bʱ��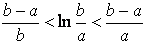 ���ɲ���֤�������������ԺͿɵ��ԣ�
���ɲ���֤�������������ԺͿɵ��ԣ�
�⣺(1)��Ϊf��(x)=3mx2+2nx,
����֪��f��(2)=0,����3m+n=0��n=-3m
��f��(x)=3mx2-6mx,��f��(x)>0֪mx(x-2)>0.
��m>0ʱ��x<0��x>2��f(x)�ļ�����Ϊ��0��2����
��m<0ʱ�ã�0<x<2,f(x)�ļ�����Ϊ��-�ޣ�0���ͣ�2��+�ޣ���
������������m>0ʱ��f(x)�ļ�����Ϊ��0��2����
��m<0ʱ,f(x)�ļ�����Ϊ��-�ޣ�0���ͣ�2��+�ޣ���

�ɻ�Ϊ3x2-6x-x12-x22-x1x2+3x1+3x2=0,��h(x)= 3x2-6x-x12-x22-x1x2+3x1+3x2-
��h(x1)=(x1-x2)(2x1+x2-3),h(x2)=(x2-x1)(x1+2x2-3),
��h(x1)h(x2)=-(x1-x2)2(2x1+x2-3)(x1+2x2-3) ����Ϊ0<x1<x2<1,����(2x1+x2-3)<0,(x1+2x2-3)<0, ��h(x1)h(x2)<0, -
��h(x)=0������(x1,x2)�ڱ��н⣬
������x�ķ���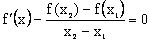 �ڣ�x1,x2������ʵ����-
�ڣ�x1,x2������ʵ����-
��3����g(x)=lnx,x��(a,b)�� -----------10��
��g(x)��������������ֵ����������,������x0�ʣ�a,b��,ʹ
��Ϊg��(x)=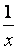 ,��x��(a,b),0<a<b��֪g��(x)��(
,��x��(a,b),0<a<b��֪g��(x)��(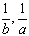 ),b-a>0
),b-a>0
��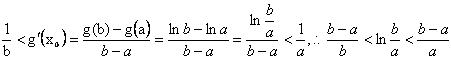

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�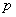 :������ʵ��
:������ʵ��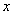 ������ʽ
������ʽ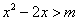 �����������
�����������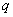 :����
:����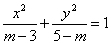 ��ʾ������
��ʾ������ ��ȡֵ��Χ��
��ȡֵ��Χ��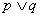 ��Ϊ�����⣬�ҡ�
��Ϊ�����⣬�ҡ�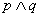 ��Ϊ�����⣬��ʵ��
��Ϊ�����⣬��ʵ�� ��(3����4)��
��(3����4)�� ��(6����3)��
��(6����3)�� ��(5��m����3��m)������ABCΪ��ǣ���ʵ��m��ȡֵ��Χ .
��(5��m����3��m)������ABCΪ��ǣ���ʵ��m��ȡֵ��Χ . ����ȡ��ֵΪ1��2��3��4��
����ȡ��ֵΪ1��2��3��4�� ��
�� 1��2��3��4��.
1��2��3��4��. .
.
 ��
�� ��
�� ��
�� , �ң���
, �ң��� ���� ��
���� �� �ĵ���������ͺ���ͼ��ĶԳ��᷽�̣�
�ĵ���������ͺ���ͼ��ĶԳ��᷽�̣� }�У���֪
}�У���֪
 ,��nΪ ( )
,��nΪ ( ) �Ľ�������б��Ϊ
�Ľ�������б��Ϊ ֱ��
ֱ�� ��ֱ��
��ֱ�� ��
�� ���㣬����
���㣬���� �ij��� .
�ij��� .  �ֱ��Ƕ�����
�ֱ��Ƕ����� �ϵ��溯����ż����,��
�ϵ��溯����ż����,�� ʱ��
ʱ�� ����
���� ����ʽ
����ʽ �Ľ⼯�ǣ� ��
�Ľ⼯�ǣ� �� B.
B. 
 D.
D. 
