题目内容
3.f(x)的定义域为[-1,2],则f(2x+1)的定义域是[-1,$\frac{1}{2}$].分析 利用函数的定义域,列出不等式求解即可.
解答 解:f(x)的定义域为[-1,2],
可得-1≤2x+1≤2,
解得:-1≤x≤$\frac{1}{2}$.
则f(2x+1)的定义域是:[-1,$\frac{1}{2}$]
点评 本题考查抽象函数的定义域的求法,是基础题.

练习册系列答案
相关题目
14.在△ABC中,a,b,c分别为角A、B、C的对边,若a=2,b=2$\sqrt{3}$,∠A=30°,则∠B等于( )
| A. | 30° | B. | 30°或150° | C. | 60° | D. | 60°或120° |
15.函数$f(x)=\sqrt{4-x}+lg\frac{{{x^2}-5x+6}}{x-3}$的定义域为( )
| A. | (2,3) | B. | (2,4) | C. | (2,3)∪(3,4] | D. | (-1,3)∪(3,6] |
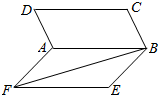 如图,四边形ABCD与四边形ABEF都是正方形,且二面角D-AB-F的大小为60°,则异面直线AD与BF所成角的余弦值是$\frac{\sqrt{2}}{4}$.
如图,四边形ABCD与四边形ABEF都是正方形,且二面角D-AB-F的大小为60°,则异面直线AD与BF所成角的余弦值是$\frac{\sqrt{2}}{4}$.