题目内容
12.已知向量$\vec a$=(sinθ,cosθ),$\vec b$=(1,-2),满足$\vec a⊥\vec b$.(1)求tanθ的值;
(2)求$\frac{{\sqrt{2}sin(θ+\frac{π}{4})(sinθ+2cosθ)}}{cos2θ}$的值.
分析 (1)由向量垂直求出sinθ=2cosθ,由此能求出tanθ.
(2)利用正弦加法定理和余弦二倍角公式把原式转化为$\frac{sinθ+2cosθ}{cosθ-sinθ}$,再利用同角三角函数关系式能求出结果.
解答 解:(1)∵$\vec a$=(sinθ,cosθ),$\vec b$=(1,-2),满足$\vec a⊥\vec b$,
∴$\overrightarrow{a}•\overrightarrow{b}$=sinθ-2cosθ=0,
∴sinθ=2cosθ,
∴tanθ=$\frac{sinθ}{cosθ}$=2
(2)$\frac{{\sqrt{2}sin(θ+\frac{π}{4})(sinθ+2cosθ)}}{cos2θ}$
=$\frac{\sqrt{2}(\frac{\sqrt{2}}{2}sinθ+\frac{\sqrt{2}}{2}cosθ)}{(cosθ+sinθ)(cosθ-sinθ)}$
=$\frac{sinθ+2cosθ}{cosθ-sinθ}$
=$\frac{tanθ+2}{1-tanθ}$
=$\frac{2+2}{1-2}$=-4.
点评 本题考查三角函数化简求值,是中档题,解题时要注意向量垂直、正弦加法定理、余弦二倍角公式、同角三角函数关系式的合理运用.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
17.下列函数中,定义域为(0,+∞)的是( )
| A. | $y=\frac{1}{{\sqrt{x}}}$ | B. | y=x+1 | C. | $y=\frac{1}{x^2}$ | D. | y=2x |
4.在区间(-∞,0)上为增函数的是( )
| A. | y=-x | B. | y=$\frac{x}{1-x}$+2 | C. | y=-x2-2x-1 | D. | y=x2+1 |
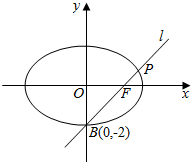 如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个顶点为B(0,-2),斜率为1的直线l过它的右焦点F,且与椭圆相交于B、P两点.求:
如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个顶点为B(0,-2),斜率为1的直线l过它的右焦点F,且与椭圆相交于B、P两点.求: