题目内容
13.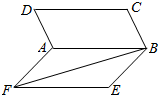 如图,四边形ABCD与四边形ABEF都是正方形,且二面角D-AB-F的大小为60°,则异面直线AD与BF所成角的余弦值是$\frac{\sqrt{2}}{4}$.
如图,四边形ABCD与四边形ABEF都是正方形,且二面角D-AB-F的大小为60°,则异面直线AD与BF所成角的余弦值是$\frac{\sqrt{2}}{4}$.
分析 由已知得∠DAF=60°,CD⊥平面DAF,AD∥BC,∠FBC是异面直线AD与BF所成角,由此利用余弦定理能求出异面直线AD与BF所成角的余弦值.
解答 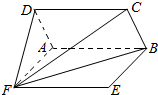 解:∵四边形ABCD与四边形ABEF都是正方形,且二面角D-AB-F的大小为60°,
解:∵四边形ABCD与四边形ABEF都是正方形,且二面角D-AB-F的大小为60°,
∴∠DAF=60°,CD⊥平面DAF,AD∥BC,
设AB=a,则DF=a,FC=BF=$\sqrt{{a}^{2}+{a}^{2}}$=$\sqrt{2}a$,
∵AD∥BC,∴∠FBC是异面直线AD与BF所成角,
由余弦定理得cos∠FBC=$\frac{B{F}^{2}+B{C}^{2}-C{F}^{2}}{2•BF•BC}$=$\frac{2{a}^{2}+{a}^{2}-2{a}^{2}}{2•\sqrt{2}a•a}$=$\frac{\sqrt{2}}{4}$.
∴异面直线AD与BF所成角的余弦值是$\frac{\sqrt{2}}{4}$.
故答案为:$\frac{\sqrt{2}}{4}$.
点评 本题考查异面直线所成角的余弦值的求法,是中档题,解题时要注意空间思维能力的培养.

练习册系列答案
相关题目
8.如图,ABCD-A1B1C1D1为正方体,下面结论错误的是( )
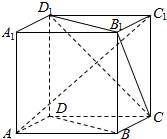

| A. | BD∥平面CB1D1 | B. | AC1⊥BD | ||
| C. | 异面直线AD与CB1角为60° | D. | AC1⊥平面CB1D1 |