题目内容
13.已知函数f(x)=$\frac{(x-1)|x|}{|{x}^{2}-1|}$.(1)写出函数定义域;
(2)在直角坐标系中画出函数f(x)的图象的大致形状;
(3)根据图形,指出函数的奇偶性,函数单调区间.
分析 (1)根据分母不能为零,即可求出函数的定义域,
(2)去绝对值,化为分段函数,再作图,
(3)由图象可知答案.
解答 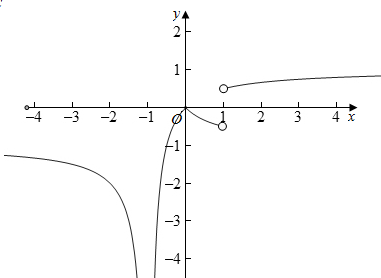 解:(1)函数的定义域为(-∞,-1)∪(-1,1)∪(1,+∞);
解:(1)函数的定义域为(-∞,-1)∪(-1,1)∪(1,+∞);
(2)f(x)=$\frac{(x-1)|x|}{|{x}^{2}-1|}$=$\left\{\begin{array}{l}{\frac{x}{x+1},x>1,或-1<x<0}\\{-\frac{x}{x+1},0≤x<1,或x<-1}\end{array}\right.$,图象如图所示,
(3)由图象可知,函数为非奇非偶函数,
f(x)在(-1,0)和(1,+∞)为增函数,在(0,1)和(-∞,-1)为减函数.
点评 本题考查了函数图象的作法和识别以及函数的定义域,关键是去绝对值,化为分段函数,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.在区间(-∞,0)上为增函数的是( )
| A. | y=-x | B. | y=$\frac{x}{1-x}$+2 | C. | y=-x2-2x-1 | D. | y=x2+1 |
18.对函数f(x),若对于定义域中的任意三个数x1,x2,x3,都有f(x1),f(x2),f(x3)都能作为一个三角形三边的长,则称f(x)为“三角型函数”.已知函数f(x)=$\frac{{9}^{x}+m•{3}^{x}+1}{{9}^{x}+{3}^{x}+1}$为“三角型函数”.则实数m的取值范围是( )
| A. | [1,4] | B. | (-$\frac{1}{2}$,1) | C. | [-$\frac{1}{2}$,4] | D. | [1,2] |
17.偶函数f(x)在区间[1,4]上为减函数,则它在区间[-4,-1]上( )
| A. | 是增函数 | B. | 是减函数 | C. | 无法确定 | D. | 不具备单调性 |
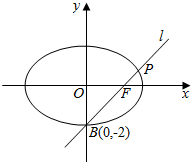 如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个顶点为B(0,-2),斜率为1的直线l过它的右焦点F,且与椭圆相交于B、P两点.求:
如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个顶点为B(0,-2),斜率为1的直线l过它的右焦点F,且与椭圆相交于B、P两点.求: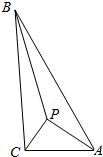 如图,在△ABC中,∠C=90°,P为三角形内一点,且S△PAB=S△PBC=S△PCA,求证:|PA|2+|PB|2=5|PC|2.
如图,在△ABC中,∠C=90°,P为三角形内一点,且S△PAB=S△PBC=S△PCA,求证:|PA|2+|PB|2=5|PC|2.