题目内容
18.某高校在2015年的自主招生考试成绩中随机抽取100名学生的笔试成绩,成绩都为整数且全部分布在[160,185].按成绩分5组[160,165),[165,170),[170,175),[175,180),[180,185],画出如下部分频率分布直方图.观察图形,根据给出的信息,回答下列问题: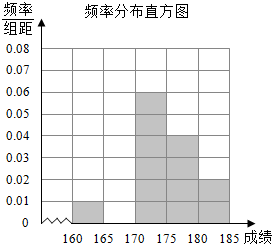
(1)求第二小组的频率,并补全这个频率分布直方图;
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样选取6名学生进入第二轮面试,求:
①第3、4、5组每组各选取多少名学生进入第二轮面试?
②高校决定从参加二轮面试的6名学生中随机选派2名到北京大学学习交流,求这两人在同一分数段的概率.
分析 (1)利用$\frac{频率}{组距}=0.07$,然后画出频率分布直方图.
(2)求出第3、4、5组分别抽取3人、2人、1人.基本事件构成集合Ω元素个数,在同一分数段内的事件所含基本事件个数,求出概率.
解答 解:(1)因为各组的频率和等于1,故第2组的频率:f2=1-(0.01+0.06+0.04+0.02)×5=0.35
$\frac{频率}{组距}=0.07$
其频率分布直方图如图所示.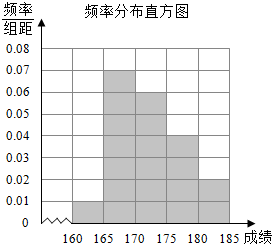
(2)因为第3、4、5组共有60名学生,所以利用分层抽样在60名学生中抽取6名学生,每组分别为:
第3组:$\frac{30}{60}×6=3$人,第4组:$\frac{20}{60}×6=2$人,
第5组:$\frac{10}{60}×6=1$人,
所以第3、4、5组分别抽取3人、2人、1人.
将[170,175)分数段的3人编号为A、B、C,将[50,60)[175,180)分数段的2人编号1、2,[180,185]分数段的1人编号为P从中任取两人,则基本事件构成集合Ω={{A,B},{A,C}{A,1},{A,2},{A,P},{B,C},{B,1},{B,2},{B,P},{C,1},{C,2},{C,P},{1,2},{1,P},{2,P}}共有15个,其中,在同一分数段内的事件所含基本事件为{A,B},{A,C}{B,C},{1,2},共4个,故概率$p=\frac{4}{15}$.
点评 本题考查频率分布直方图的应用,古典概型概率的求法,是基础题.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
8.如图,ABCD-A1B1C1D1为正方体,下面结论错误的是( )
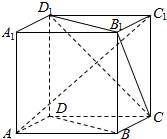

| A. | BD∥平面CB1D1 | B. | AC1⊥BD | ||
| C. | 异面直线AD与CB1角为60° | D. | AC1⊥平面CB1D1 |
9.与圆O1:x2+y2=1和圆O2:x2+y2-6x-8y+9=0都相切的直线条数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
10.“x≥0”是“log${\;}_{\frac{1}{2}}$(x+2)<2”的( )
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
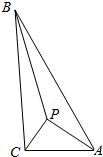 如图,在△ABC中,∠C=90°,P为三角形内一点,且S△PAB=S△PBC=S△PCA,求证:|PA|2+|PB|2=5|PC|2.
如图,在△ABC中,∠C=90°,P为三角形内一点,且S△PAB=S△PBC=S△PCA,求证:|PA|2+|PB|2=5|PC|2.