题目内容
如右数阵共有10列，其中第一行的数是首项为1，公差为1的等差数列；第二行的数是首项为第一行第十列的数加上2，公差为2的等差数列；第三行的数是首项为第二行第十列的数加上4，公差为4的等差数列，…，第n行的数是首项为第n-1行第十列的数加上2（n-1），公差为2（n-1）的等差数列，则第n行第7列的数为 ．（用表示）
| 1 | 2 | 3 | … | 5 |
| 12 | 14 | 16 | … | 30 |
| 34 | 38 | 42 | … | … |
| … | … | … | … | … |
考点：等差数列的性质
专题：计算题,等差数列与等比数列
分析：通过归纳得到第n行第一列为1+9×[1+2+…+2（n-2）]+[2+4+…+2（n-1）]，化简得到10n2-28n+28．再由等差数列的通项公式，即可得到第n行第7列的数．
解答：
解：由题意可得，第一行第一列为10，
第二行第一列为1+9×1+2=12；
第三行第一列为12+9×2+4=34，
第四行第一列为34+9×4+6=76；
…
第n行第一列为1+9×[1+2+…+2（n-2）]+[2+4+…+2（n-1）]
=1+9×[1+（n-1）（n-2）]+n（n-1）=10n2-28n+28．
则有第n行第7列的数为10n2-28n+28+6×2（n-1）=10n2-16n+16．
故答案为：10n2-16n+16（n≥2）．
第二行第一列为1+9×1+2=12；
第三行第一列为12+9×2+4=34，
第四行第一列为34+9×4+6=76；
…
第n行第一列为1+9×[1+2+…+2（n-2）]+[2+4+…+2（n-1）]
=1+9×[1+（n-1）（n-2）]+n（n-1）=10n2-28n+28．
则有第n行第7列的数为10n2-28n+28+6×2（n-1）=10n2-16n+16．
故答案为：10n2-16n+16（n≥2）．
点评：本题考查等差数列的通项公式和求和公式的运用，考查推理能力和运算能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
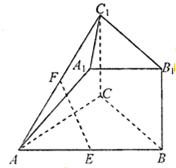在如图所示的几何体中，四边形BB1C1C是长方形，BB1⊥AB，CA=CB，