题目内容
已知向量
、
满足|
|=
，|
|=6，
与
的夹角为
，则3|
|-2（
•
）+4|
|= ．
| a |
| b |
| a |
| 1 |
| 3 |
| b |
| a |
| b |
| π |
| 3 |
| a |
| a |
| b |
| b |
考点：平面向量数量积的运算
专题：计算题,平面向量及应用
分析：运用向量的数量积的定义计算向量a，b的数量积，代入数据计算即可得到．
解答：
解：向量
、
满足|
|=
，|
|=6，
与
的夹角为
，
则
•
=|
|•|
|•cos
=
×6×
=1，
则有3|
|-2（
•
）+4|
|=3×
-2×1+4×6=23．
故答案为：23．
| a |
| b |
| a |
| 1 |
| 3 |
| b |
| a |
| b |
| π |
| 3 |
则
| a |
| b |
| a |
| b |
| π |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
则有3|
| a |
| a |
| b |
| b |
| 1 |
| 3 |
故答案为：23．
点评：本题考查向量的数量积的定义和性质，考查运算能力，属于基础题．
练习册系列答案
相关题目
设集合M={x|x 2+3x+2＜0}，集合N={x|（
）x≤4}，则 M∪N=（ ）
| 1 |
| 2 |
| A、{ x|x≥-2} |
| B、{ x|x＞-1} |
| C、{ x|x＜-1} |
| D、{ x|x≤-2} |
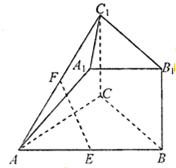在如图所示的几何体中，四边形BB1C1C是长方形，BB1⊥AB，CA=CB，
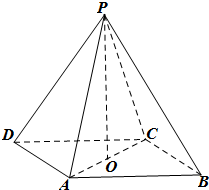如图，在四棱锥P-ABCD中，底面ABCD为平行四边形，∠DAC=90°，O为AC的中点，PO⊥底面ABCD．