题目内容
同时抛掷两枚骰子,没有5点或6点的概率是
,则至少一个5点或6点的概率是 .
| 4 |
| 9 |
考点:互斥事件与对立事件
专题:概率与统计
分析:根据对立事件的概率公式求解即可.
解答:
解:同时抛掷两枚骰子,“没有5点或6点”的对立事件是“至少一个5点或6点”的事件,
又没有5点或6点的概率是
,
则至少一个5点或6点的概率1-
=
,
故答案为:
又没有5点或6点的概率是
| 4 |
| 9 |
则至少一个5点或6点的概率1-
| 4 |
| 9 |
| 5 |
| 9 |
故答案为:
| 5 |
| 9 |
点评:本题主要考查对立事件与互斥事件的概念,属于基础题

练习册系列答案
相关题目
有三个游戏规则如下,袋子中分别装有形状、大小相同的球,从袋中无放回地取球,
问其中不公平的游戏是( )
| 游戏1 | 游戏2 | 游戏3 |
| 袋中装有3个黑球和2个白球 | 袋中装有2个黑球和2个白球 | 袋中装有3个黑球和1个白球 |
| 从袋中取出2个球 | 从袋中取出2个球 | 从袋中取出2个球 |
| 若取出的两个球同色,则甲胜 | 若取出的两个球同色,则甲胜 | 若取出的两个球同色,则甲胜 |
| 若取出的两个球不同色,则乙胜 | 若取出的两个球不同色,则乙胜 | 若取出的两个球不同色,则乙胜 |
| A、游戏2 |
| B、游戏3 |
| C、游戏1和游戏2 |
| D、游戏1和游戏3 |
已知集合M={2,4,6,8},N={1,2},P={x|x=
,a∈M,b∈N},则集合P的真子集的个数为( )
| a |
| b |
| A、4 | B、6 | C、15 | D、63 |
若点P(-
,m)是角θ终边上一点,且sinθ=
,则m的值为( )
| 3 |
| ||
| 3 |
A、
| ||||
B、±
| ||||
C、
| ||||
D、±
|
在数列{an}中,若a1=2,an+1=an+ln(1+
),则an等于( )
| 1 |
| n |
| A、2+ln2 |
| B、2+(n-1)lnn |
| C、2+nlnn |
| D、1+n |
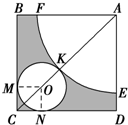 如图所示,在边长为5+
如图所示,在边长为5+