题目内容
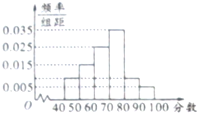 从参加环保知识竞赛的学生中抽取40名,将其成绩(均为整数)整理后画出频率分布直方图如图.估计这次环保知识竞赛成绩的中位数为
从参加环保知识竞赛的学生中抽取40名,将其成绩(均为整数)整理后画出频率分布直方图如图.估计这次环保知识竞赛成绩的中位数为考点:频率分布直方图
专题:概率与统计
分析:先根据各组频率和(矩形面积和)为1,确定第二组及第五组数据对应矩形的高,进而求出各组的频率,再根据中位数平分矩形面积,得到竞赛成绩的中位数;计算出80分以上(包括80分)的学生中任选两人的基本事件总数及他们在同一分数段的基本事件个数,代入古典概型概率计算公式,可得答案.
解答:
解:设第二组及第五组数据对应矩形的高为a,
则10×(a+0.015+0.025+0.035+a+0.005)=1,
解得a=0.010,
故各组的频率依次为:0.10,0.15,0.25,0.35,0.10,0.05,
∵前三组的累积频率为:0.10+0.15+0.25=0.50,
故这次环保知识竞赛成绩的中位数为70;
成绩在[80,90)段的人数有10×0.010×40=4人,
成绩在[90,100]段的人数有10×0.005×40=2人,
从成绩是80分以上(包括80分)的学生中任选两人共有
=15种不同的基本事件,
其中他们在同一分数段的基本事件有:
+
=7,
故他们在同一分数段的概率为
,
故答案为:70,
.
则10×(a+0.015+0.025+0.035+a+0.005)=1,
解得a=0.010,
故各组的频率依次为:0.10,0.15,0.25,0.35,0.10,0.05,
∵前三组的累积频率为:0.10+0.15+0.25=0.50,
故这次环保知识竞赛成绩的中位数为70;
成绩在[80,90)段的人数有10×0.010×40=4人,
成绩在[90,100]段的人数有10×0.005×40=2人,
从成绩是80分以上(包括80分)的学生中任选两人共有
| C | 2 6 |
其中他们在同一分数段的基本事件有:
| C | 2 4 |
| C | 2 2 |
故他们在同一分数段的概率为
| 7 |
| 15 |
故答案为:70,
| 7 |
| 15 |
点评:本题考查的知识点是古典概型概率计算公式,其中熟练掌握利用古典概型概率计算公式求概率的步骤,是解答的关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
已知θ为锐角,且sin(θ-
)=
,在tanθ=( )
| π |
| 4 |
| ||
| 10 |
A、
| ||
B、
| ||
C、-
| ||
D、
|
 已知某个几何体的三视图如下(主视图的弧线是半圆),根据图中标出的尺寸(单位:cm),可得这个几何体的体积是
已知某个几何体的三视图如下(主视图的弧线是半圆),根据图中标出的尺寸(单位:cm),可得这个几何体的体积是