题目内容
已知θ为锐角,且sin(θ-
)=
,在tanθ=( )
| π |
| 4 |
| ||
| 10 |
A、
| ||
B、
| ||
C、-
| ||
D、
|
考点:两角和与差的正弦函数
专题:计算题,三角函数的求值
分析:可求cos(θ-
),进而可求tan(θ-
),而tanθ=tan[(θ-
)+
],利用和角的正切公式即可求得.
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
解答:
解:∵θ为锐角,∴-
<θ-
<
,
∴cos(θ-
)=
=
=
,
∴tan(θ-
)=
=
,
∴tanθ=tan[(θ-
)+
]=
=
=
,
故选A.
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
∴cos(θ-
| π |
| 4 |
1-sin2(θ-
|
1-(
|
7
| ||
| 10 |
∴tan(θ-
| π |
| 4 |
sin(θ-
| ||
cos(θ-
|
| 1 |
| 7 |
∴tanθ=tan[(θ-
| π |
| 4 |
| π |
| 4 |
tan(θ-
| ||||
1-tan(θ-
|
| ||
1-
|
| 4 |
| 3 |
故选A.
点评:该题考查两角和与差是正切公式、正弦公式,考查学生灵活运用相关公式解决问题的能力,属基础题.

练习册系列答案
相关题目
已知
=(2,3,4),
=(6,x,y),若
∥
,则x+y的值是( )
| a |
| b |
| a |
| b |
| A、14 | B、16 | C、21 | D、26 |
数列{an}由a1=1,an+1=an+n(n∈N*)确定,则通项公式为( )
A、an=
| ||
B、an=
| ||
C、an=
| ||
D、an=
|
已知曲线C:y=(ax2+2x+3)ex存在两点处的切线互相平行,则a的取值范围为( )
| A、a>1 | ||
B、a<
| ||
C、a≤
| ||
D、a>1或a<
|
已知{an}为等差数列,若a1+a9=
,则cos(a3+a7)的值为( )
| π |
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
已知a>0,b<-1,则下列不等式成立的是( )
A、a>-
| ||||
B、
| ||||
C、-
| ||||
D、-
|
在△ABC中,A=
,C=
,b=2,那么a=( )
| π |
| 6 |
| 7π |
| 12 |
A、
| ||
| B、2 | ||
C、2
| ||
| D、1 |
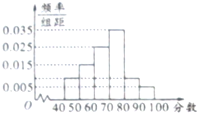 从参加环保知识竞赛的学生中抽取40名,将其成绩(均为整数)整理后画出频率分布直方图如图.估计这次环保知识竞赛成绩的中位数为
从参加环保知识竞赛的学生中抽取40名,将其成绩(均为整数)整理后画出频率分布直方图如图.估计这次环保知识竞赛成绩的中位数为