题目内容
有4个不同的球,四个不同的盒子,把球全部放入盒内.恰有两个盒不放球,有多少种放法?答案 (结果用数字表示)
考点:排列、组合及简单计数问题
专题:应用题,排列组合
分析:四个不同的球全部放入4个不同的盒子内,恰有两个盒子不放球的不同放法的求法,分为两步来求解,先把四个球分为两组,再取两个盒子,作全排列,由于四个球分两组有两种分法,一种是2,2,另一种是3,1,故此题分为两类来求解,再求出它们的和,然后选出正确选项.
解答:
解:四个球分为两组有两种分法,(2,2),(3,1)
若两组每组有两个球,不同的分法有
=3种,恰有两个盒子不放球的不同放法是3×A42=36种
若两组一组为3,一组为1个球,不同分法有C43=4种恰有两个盒子不放球的不同放法是4×A42=48种
综上,恰有两个盒子不放球的不同放法是36+48=84种.
故答案为:84.
若两组每组有两个球,不同的分法有
| ||
|
若两组一组为3,一组为1个球,不同分法有C43=4种恰有两个盒子不放球的不同放法是4×A42=48种
综上,恰有两个盒子不放球的不同放法是36+48=84种.
故答案为:84.
点评:本题考查排列、组合的实际应用,解题的关键是理解事件“四个不同的球全部放入4个不同的盒子内,恰有两个盒子不放球”,宜先将四个球分为两组,再放入,分步求不同的放法种数.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目

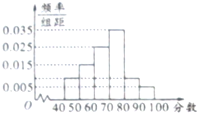 从参加环保知识竞赛的学生中抽取40名,将其成绩(均为整数)整理后画出频率分布直方图如图.估计这次环保知识竞赛成绩的中位数为
从参加环保知识竞赛的学生中抽取40名,将其成绩(均为整数)整理后画出频率分布直方图如图.估计这次环保知识竞赛成绩的中位数为