题目内容
在平面直角坐标系xOy中,圆C的参数方程为
(θ为参数,r>0),以O为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为ρsin(θ+
).
(Ⅰ)求圆C的普通方程和直线l的直角坐标方程;
(Ⅱ)若圆C上的点到直线l的最大距离为3,求r的值.
|
| π |
| 4 |
(Ⅰ)求圆C的普通方程和直线l的直角坐标方程;
(Ⅱ)若圆C上的点到直线l的最大距离为3,求r的值.
考点:参数方程化成普通方程,直线与圆的位置关系
专题:选作题,坐标系和参数方程
分析:(Ⅰ)将直线l的参数方程的参数t消去即可求出直线的普通方程,利用极坐标转化成直角坐标的转换公式求出圆的直角坐标方程;
(Ⅱ)若圆C上的点到直线l的最大距离为3,即d+r=3,即可求r的值.
(Ⅱ)若圆C上的点到直线l的最大距离为3,即d+r=3,即可求r的值.
解答:
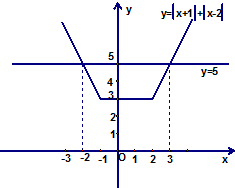 解:(Ⅰ)因为圆C的参数方程为
解:(Ⅰ)因为圆C的参数方程为
(θ为参数,r>0),消去参数得,(x+
)2+(y+
)2=r2(r>0),…(2分)
所以圆心C(-
,-
),半径为r,
因为直线l的极坐标方程为ρsin(θ+
)=1,
化为普通方程为x+y=
,…(4分)
(Ⅱ)圆心C到直线x+y=
的距离为d=
=2,…(5分)
又因为圆C上的点到直线l的最大距离为3,即d+r=3,所以r=3-2=1…(7分)
 解:(Ⅰ)因为圆C的参数方程为
解:(Ⅰ)因为圆C的参数方程为
|
| ||
| 2 |
| ||
| 2 |
所以圆心C(-
| ||
| 2 |
| ||
| 2 |
因为直线l的极坐标方程为ρsin(θ+
| π |
| 4 |
化为普通方程为x+y=
| 2 |
(Ⅱ)圆心C到直线x+y=
| 2 |
|-
| ||||||||||
|
又因为圆C上的点到直线l的最大距离为3,即d+r=3,所以r=3-2=1…(7分)
点评:本题主要考查了简单曲线的极坐标方程,以及直线的参数方程和直线与圆的位置关系的判定,属于基础题.

练习册系列答案
相关题目
已知
=(2,3,4),
=(6,x,y),若
∥
,则x+y的值是( )
| a |
| b |
| a |
| b |
| A、14 | B、16 | C、21 | D、26 |
已知a>0,b<-1,则下列不等式成立的是( )
A、a>-
| ||||
B、
| ||||
C、-
| ||||
D、-
|
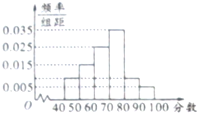 从参加环保知识竞赛的学生中抽取40名,将其成绩(均为整数)整理后画出频率分布直方图如图.估计这次环保知识竞赛成绩的中位数为
从参加环保知识竞赛的学生中抽取40名,将其成绩(均为整数)整理后画出频率分布直方图如图.估计这次环保知识竞赛成绩的中位数为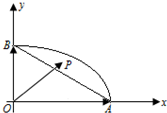 A,B是椭圆的右顶点及上顶点,由椭圆弧
A,B是椭圆的右顶点及上顶点,由椭圆弧