题目内容
已知点A(-5,0),B(-1,-3),若圆x2+y2=r2(r>0)上恰有两点M,N,使得△MAB和△NAB的面积均为5,则r的取值范围是 .
考点:直线与圆的位置关系
专题:直线与圆
分析:先求得|AB|=5,根据题意可得两点M,N到直线AB的距离为2.求出AB的方程为3x+4y+15=0,当圆上只有一个点到直线AB的距离为2 时,求得r的值;当圆上只有3个点到直线AB的距离为2时,求得r的值,从而求得满足条件的r的取值范围.
解答:
解:由题意可得|AB|=
=5,根据△MAB和△NAB的面积均为5,
可得两点M,N到直线AB的距离为2.
由于AB的方程为
=
,即 3x+4y+15=0.
若圆上只有一个点到直线AB的距离为2,
则有圆心(0,0)到直线AB的距离
=r+2,解得r=1.
若圆上只有3个点到直线AB的距离为2,
则有圆心(0,0)到直线AB的距离
=r-2,解得r=5,
故答案为:(1,5).
| (-1+5)2+(-3-0)2 |
可得两点M,N到直线AB的距离为2.
由于AB的方程为
| y-0 |
| -3-0 |
| x+5 |
| -1+5 |
若圆上只有一个点到直线AB的距离为2,
则有圆心(0,0)到直线AB的距离
| |0+0+15| | ||
|
若圆上只有3个点到直线AB的距离为2,
则有圆心(0,0)到直线AB的距离
| |0+0+15| | ||
|
故答案为:(1,5).
点评:本题主要考查直线和圆的位置关系,点到直线的距离公式的应用,属于基础题.

练习册系列答案
相关题目
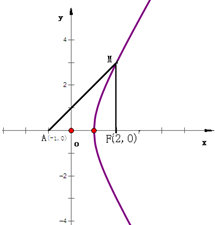 已知曲线C:x2-
已知曲线C:x2-
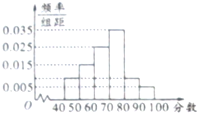 从参加环保知识竞赛的学生中抽取40名,将其成绩(均为整数)整理后画出频率分布直方图如图.估计这次环保知识竞赛成绩的中位数为
从参加环保知识竞赛的学生中抽取40名,将其成绩(均为整数)整理后画出频率分布直方图如图.估计这次环保知识竞赛成绩的中位数为