题目内容

已知某个几何体的三视图如下（主视图的弧线是半圆），根据图中标出的尺寸（单位：cm），可得这个几何体的体积是
 
cm3．
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：由已知中的三视图，可得该几何体是一个以正视图为底面的柱体，求出柱体的底面面积和高，代入柱体体积公式，可得答案．
解答： 解：由已知中的三视图，可得该几何体是一个以正视图为底面的柱体，
柱体的底面积S=6×6+
1
2
π×32=36+
9
2
πcm2．
柱体的高h=6cm．
故柱体的体积V=Sh=216+27πcm3．
故答案为：216+27π．
点评：本题考查的知识点是由三视图求体积，其中分析出几何体的形状是解答的关键．
练习册系列答案
相关题目
观察下列等式：
C
0
5
+
C
4
5
=23-2，
C
0
9
+
C
4
9
+
C
8
9
=27+23，
C
0
13
+
C
4
13
+
C
8
13
+
C
12
13
=211-25，
C
0
17
+
C
4
17
+
C
8
17
+
C
12
17
+
C
16
17
=215+27，
…
由以上等式推测到一个一般的结论为：对于n∈N*，
C
0
4n+1
+
C
4
4n+1
+
C
8
4n+1
+…+
C
4n
4n+1
=
 
．
用弧度表示第一或第三象限角的集合
 
．
设曲线C的参数方程为
x=cosθ
y=2sin2θ
 （θ为参数），一直角坐标系的原点为极点，x轴的正半轴为极轴，且两种坐标系中坐标轴上的单位长度相同，已知直线l的极坐标方程是θ=
π
3
，则曲线C与直线l的交点坐标是
 
．
已知等差数列{an}的前n项和Sn有最小值，且a3+a5=14，a2a6=33，则数列{
1
anan+1
}的前100项的和T100=
 
．
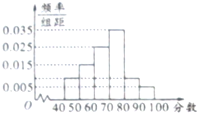从参加环保知识竞赛的学生中抽取40名，将其成绩（均为整数）整理后画出频率分布直方图如图．估计这次环保知识竞赛成绩的中位数为
 
；从成绩是80分以上（包括80分）的学生中任选两人，他们在同一分数段的概率为
 
．
某校高中年级开设了丰富多彩的校本课程，甲、乙两班各随机抽取5名学生的成绩，用茎叶图表示如下图，则甲、乙两班抽取的5名学生成绩的中位数的和等于
 
．
用数学归纳法证明不等式“
1
n+1
+
1
n+2
+
1
n+3
+…
1
3n+1
＞
25
12
”，当n=1时，不等式左边的项为
 
．
数列{an}由a1=1，an+1=an+n（n∈N*）确定，则通项公式为（　　）
A、an=
n2-n
2
B、an=
n2-n+2
2
C、an=
n2+n
2
D、an=
n2+n+2
2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网