题目内容
设Sn是公差不为零的等差数列{an}的前n项和，且S7=14a5，若am=0，则m= ．
考点：等差数列的通项公式
专题：等差数列与等比数列
分析：设出等差数列{an}的首项和公差，由S7=14a5得到首项和公差的关系，结合am=0求得m的值．
解答：
解：设等差数列{an}的首项为a1，公差为d，
由S7=14a5，得7a4=14a5，
即a4=2a5，
a1+3d=2（a1+4d），
∴a1=-5d．
由am=a1+（m-1）d=-5d+（m-1）d=0，得m=6．
故答案为：6．
由S7=14a5，得7a4=14a5，
即a4=2a5，
a1+3d=2（a1+4d），
∴a1=-5d．
由am=a1+（m-1）d=-5d+（m-1）d=0，得m=6．
故答案为：6．
点评：本题考查了等差数列的通项公式，考查了等差数列的性质，是基础题．
练习册系列答案
相关题目
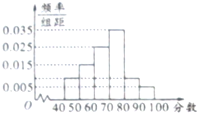从参加环保知识竞赛的学生中抽取40名，将其成绩（均为整数）整理后画出频率分布直方图如图．估计这次环保知识竞赛成绩的中位数为
某校高中年级开设了丰富多彩的校本课程，甲、乙两班各随机抽取5名学生的成绩，用茎叶图表示如下图，则甲、乙两班抽取的5名学生成绩的中位数的和等于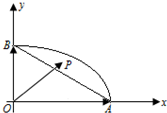
A，B是椭圆的右顶点及上顶点，由椭圆弧已知{an}为等差数列，若a1+a9=
，则cos（a3+a7）的值为（ ）
| π |
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|