题目内容
17.已知数列{an}的前n项的和Sn=$\frac{3}{2}$n2-$\frac{1}{2}$n.(1)求{an}的通项公式an;
(2)当n≥2时,an+1+$\frac{λ}{{a}_{n}}$≥λ恒成立,求实数λ的取值范围.
分析 (1)利用递推关系即可得出;
(2)变形利用基本不等式的性质即可得出.
解答 解:(1)∵Sn=$\frac{3}{2}$n2-$\frac{1}{2}$n,
∴当n=1时,a1=$\frac{3}{2}-\frac{1}{2}$=1;
当n≥2时,an=Sn-Sn-1=$\frac{3}{2}$n2-$\frac{1}{2}$n-$[\frac{3}{2}(n-1)^{2}-\frac{1}{2}(n-1)]$=3n-2.
当n=1时,上式成立,∴an=3n-2.
(2)an+1+$\frac{λ}{{a}_{n}}$≥λ,即3n+1+$\frac{λ}{3n-2}$≥λ,化为:λ≤$\frac{1}{3}$$[9(n-1)+\frac{4}{n-1}+15]$,
∵当n≥2时,an+1+$\frac{λ}{{a}_{n}}$≥λ恒成立,
∴λ≤$\frac{1}{3}[9(n-1)+\frac{4}{n-1}+15]_{min}$,
∵$[9(n-1)+\frac{4}{n-1}+15]$≥$2\sqrt{9(n-1)×\frac{4}{n-1}}$+15,
取整数n=2时,$\frac{1}{3}[9(n-1)+\frac{4}{n-1}+15]_{min}$=$\frac{28}{3}$.
∴λ≤$\frac{28}{3}$.
∴实数λ的取值范围是λ≤$\frac{28}{3}$.
点评 本题考查了递推关系、数列的单调性、基本不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.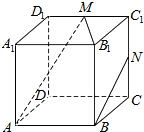 如图,在正方体ABCD-A1B1C1D1中,M、N分别为棱C1D1、C1C的中点,有以下四个结论:
如图,在正方体ABCD-A1B1C1D1中,M、N分别为棱C1D1、C1C的中点,有以下四个结论:
①直线AM与CC1是相交直线;
②直线AM与BN是平行直线;
③直线BN与MB1是异面直线;
④直线AM与DD1是异面直线.
其中正确的结论为( )
 如图,在正方体ABCD-A1B1C1D1中,M、N分别为棱C1D1、C1C的中点,有以下四个结论:
如图,在正方体ABCD-A1B1C1D1中,M、N分别为棱C1D1、C1C的中点,有以下四个结论:①直线AM与CC1是相交直线;
②直线AM与BN是平行直线;
③直线BN与MB1是异面直线;
④直线AM与DD1是异面直线.
其中正确的结论为( )
| A. | ③④ | B. | ①② | C. | ①③ | D. | ②④ |
2.下列积分均存在,则下列结论错误的是( )
| A. | d(∫f(x)dx)=f(x)dx | B. | ∫f(x)dx=∫f(u)du | ||
| C. | ${∫}_{a}^{b}$f(x)dx=${∫}_{a}^{b}$f(u)du | D. | ${∫}_{a}^{b}$f(x)dx+${∫}_{b}^{a}$f(x)dx=0. |