题目内容
12.已知函数f(x)=x2-2ax+2,x∈[-5,5](1)求实数a的取值范围,使y=f(x)在定义域上是单调递减函数;
(2)用g(a)表示函数y=f(x)的最小值,求g(a)的解析式.
分析 (1)可求出f(x)的对称轴为x=a,而要使y=f(x)在[-5,5]上单调递减,则需满足a≥5,这便得到了a的取值范围;
(2)可讨论对称轴x=a和区间[-5,5]的关系:分a≤-5,-5<a<5,和a≥5三种情况,然后根据f(x)在[-5,5]上的单调性及取得顶点情况求出每种情况的f(x)的最小值,从而便可得出g(a)的解析式.
解答 解:(1)函数f(x)的对称轴为x=a;
∵f(x)在[-5,5]上是单调递减函数;
∴a≥5;
∴实数a的取值范围为[5,+∞);
(2)①当a≤-5时,f(x)在[-5,5]上单调递增;
∴f(x)min=f(-5)=27+10a;
②当-5<a<5时,$f(x)_{min}=f(a)=-{a}^{2}+2$;
③当a≥5时,f(x)在[-5,5]上单调递减;
∴f(x)min=f(5)=27-10a;
∴$g(a)=\left\{\begin{array}{l}{27+10a}&{a≤-5}\\{-{a}^{2}+2}&{-5<a<5}\\{27-10a}&{a≥5}\end{array}\right.$.
点评 考查二次函数的对称轴,二次函数的单调性,以及根据二次函数的单调性及取得顶点情况求其在闭区间上的最小值的方法.

练习册系列答案
相关题目
2.已知直线l经过椭圆$\frac{x^2}{169}$+$\frac{y^2}{144}$=1的右焦点,与椭圆交于A(x1,y1)、B(x2,y2),若x1+x2=1,则直线l的方程为( )
| A. | 4x-13y-20=0或4x+13y-20=0 | B. | 2x-3y-10=0或2x+3y-10=0 | ||
| C. | 6x+5y-30=0或6x-5y-30=0 | D. | 4x+9y-20=0或2x+3y-10=0. |
4.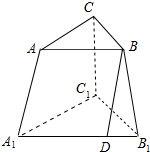 在三棱台A1B1C1-ABC中,点D在A1B1上,且AA1∥BD,点M是△A1B1C1内(含边界)的一个动点,且有平面BDM∥平面A1C,则动点M的轨迹是( )
在三棱台A1B1C1-ABC中,点D在A1B1上,且AA1∥BD,点M是△A1B1C1内(含边界)的一个动点,且有平面BDM∥平面A1C,则动点M的轨迹是( )
 在三棱台A1B1C1-ABC中,点D在A1B1上,且AA1∥BD,点M是△A1B1C1内(含边界)的一个动点,且有平面BDM∥平面A1C,则动点M的轨迹是( )
在三棱台A1B1C1-ABC中,点D在A1B1上,且AA1∥BD,点M是△A1B1C1内(含边界)的一个动点,且有平面BDM∥平面A1C,则动点M的轨迹是( )| A. | 平面 | B. | 直线 | ||
| C. | 线段,但只含1个端点 | D. | 圆 |
1.已知实数a,b,c,d满足$\frac{2+5alna}{2{a}^{2}-ab}$=$\frac{{c}^{2}-mc}{d-4}$=1,在直角坐标系中,点(a,b)和(c,d)的轨迹方程分别为y=f(x),y=g(x),若?x1∈(0,1),?x2∈[1,2],郡有f(x1)≥g(x2)成立,则实数m的最小值为( )
| A. | $\frac{11-5ln2}{2}$ | B. | 2 | C. | 8-5ln2 | D. | 7-5ln2 |
2.函数f(x)=sin(x+$\frac{π}{6}$)+cos(x+$\frac{π}{6}$)的值域是( )
| A. | [-2,2] | B. | [-1,1] | C. | [-$\sqrt{2}$,$\sqrt{2}$] | D. | [-$\frac{1}{2}$,$\frac{1}{2}$] |