题目内容
9.对于函数f(x)=1og${\;}_{\frac{1}{2}}$(x+a).(1)若函数的定义域为(-1,∞),求实数a;
(2)若a=1,解不等式f(x)>0.
分析 (1)求解函数的定义域,结合函数的定义域为(-1,+∞)可得a的值;
(2)直接求解对数不等式得答案.
解答 解:(1)由x+a>0,得x>-a,
又函数f(x)=1og${\;}_{\frac{1}{2}}$(x+a)的定义域为(-1,∞),
∴-a=-1,即a=1;
(2)当a=1时,不等式f(x)>0化为1og${\;}_{\frac{1}{2}}$(x+1)>0,
即0<x+1<1,解得-1<x<0.
∴不等式f(x)>0的解集为(-1,0).
点评 本题考查函数的定义域及其求法,考查了对数不等式的解法,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.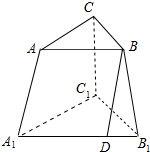 在三棱台A1B1C1-ABC中,点D在A1B1上,且AA1∥BD,点M是△A1B1C1内(含边界)的一个动点,且有平面BDM∥平面A1C,则动点M的轨迹是( )
在三棱台A1B1C1-ABC中,点D在A1B1上,且AA1∥BD,点M是△A1B1C1内(含边界)的一个动点,且有平面BDM∥平面A1C,则动点M的轨迹是( )
 在三棱台A1B1C1-ABC中,点D在A1B1上,且AA1∥BD,点M是△A1B1C1内(含边界)的一个动点,且有平面BDM∥平面A1C,则动点M的轨迹是( )
在三棱台A1B1C1-ABC中,点D在A1B1上,且AA1∥BD,点M是△A1B1C1内(含边界)的一个动点,且有平面BDM∥平面A1C,则动点M的轨迹是( )| A. | 平面 | B. | 直线 | ||
| C. | 线段,但只含1个端点 | D. | 圆 |
1.已知实数a,b,c,d满足$\frac{2+5alna}{2{a}^{2}-ab}$=$\frac{{c}^{2}-mc}{d-4}$=1,在直角坐标系中,点(a,b)和(c,d)的轨迹方程分别为y=f(x),y=g(x),若?x1∈(0,1),?x2∈[1,2],郡有f(x1)≥g(x2)成立,则实数m的最小值为( )
| A. | $\frac{11-5ln2}{2}$ | B. | 2 | C. | 8-5ln2 | D. | 7-5ln2 |
18.设三棱锥的三条侧棱两两互相垂直,且长度分别为2,2$\sqrt{3}$,4,则其外接球的表面积为( )
| A. | 48π | B. | 32π | C. | 20π | D. | 12π |