题目内容
若函数f（x）是幂函数，且满足f（2）=4，则f（
）的值为 ．
| 1 |
| 2 |
考点：幂函数的概念、解析式、定义域、值域
专题：函数的性质及应用
分析：设f（x）=xα，（α为常数）．由4=2α，可得α=2即可．
解答：
解：设f（x）=xα，（α为常数）．
∵4=2α，∴α=2．
∴f（x）=x2．
∴f(
)=(
)2=
．
故答案为：
．
∵4=2α，∴α=2．
∴f（x）=x2．
∴f(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
故答案为：
| 1 |
| 4 |
点评：本题考查了幂函数的解析式，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
设M={平面内的点（a，b）}，N={f（x）|f（x）=acos2x+bsin2x}，给出M到N的映射f：（a，b）→f（x）=acos2x+bsin2x，则点（1，
）的象f（x）的最小正周期为（ ）
| 3 |
A、
| ||
B、
| ||
| C、π | ||
| D、2π |
若非整实数x、y、z满足：2x=3y=6z．则．
A、
| ||
B、
| ||
C、
| ||
D、
|
已知全集U=R，A={x|x≤0}，B={x|x＞-1}，则集合∁U（A∩B）=（ ）
| A、{x|-1＜x≤0} |
| B、{x|-1≤x≤0} |
| C、{x|x≤-1或x≥0} |
| D、{x|x≤-1或x＞0} |
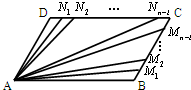已知平行四边形ABCD，点M1，M2，M3，…，Mn-1和N1，N2，N3，…，Nn-1分别将线段BC和DC，n等分（n∈N*，n≥2），如图，若