题目内容
已知函数f(x)=(4x2-4ax+a2)
,其中a>0.
(I)当a=4时,求f(x)的单调递减区间;
(Ⅱ)若f(x)在区间[1,4]上的最小值为8,求a的值.
| x |
(I)当a=4时,求f(x)的单调递减区间;
(Ⅱ)若f(x)在区间[1,4]上的最小值为8,求a的值.
考点:函数的单调性及单调区间,函数的最值及其几何意义
专题:计算题,函数的性质及应用,导数的综合应用
分析:(Ⅰ)当a=4时,先求导,在根据导数求出f(x)的单调递减区间;
(Ⅱ)利用导数判断函数的单调性,从而得出函数在闭区间上的最小值,即得到参数的一个方程,从而求出参数的值.
(Ⅱ)利用导数判断函数的单调性,从而得出函数在闭区间上的最小值,即得到参数的一个方程,从而求出参数的值.
解答:
解;(Ⅰ)当a=4时,f(x)=(4x2-16x+16)
,
∴f′(x)=(8x-16)
+(4x2-16x+16)
=2
(5x+
-12)=
(5x2-12x+4),
∵f′(x)<0,x≥0,
∴5x2-12x+4<0
解得,
<x<2,
∴f(x)的单调递减区间为(
,2);
(Ⅱ)∵f(x)=(4x2-4ax+a2)
∴f′(x)=
(20x2-12ax+a2)
令f′(x)=0.解得x=
或
,
当f′(x)>0时,x在(0,
),(
,+∞)为单调递增,
当f′(x)<0时,x在(
,
)上单调递减,
①当
≥4,即a≥40,f(x)在区间[1,4]为增函数,
由f(1)=8,解得a=2±2
,不符合舍去.
②当
≤1,即0<a≤2时,f(x)在区间[1,4]为增函数,
由f(1)=8,解得a=2±2
,不符合舍去.
③当
≤1,且
≥4,即8≤a≤10时,f(x)在区间[1,4]为减函数,
由f(4)=8,解得a=10,
④当1<
<4,即10<a<40时,由f(1)=8或f(4)=8,
解得,a=2±2
,或a=6,a=10,不符合舍去,
⑤当1<
<4,即4<a<8时,由f(
)=8,无解.
综上所述,a=10.
| x |
∴f′(x)=(8x-16)
| x |
| 1 | ||
2
|
=2
| x |
| 4 |
| x |
2
| ||
| x |
∵f′(x)<0,x≥0,
∴5x2-12x+4<0
解得,
| 2 |
| 5 |
∴f(x)的单调递减区间为(
| 2 |
| 5 |
(Ⅱ)∵f(x)=(4x2-4ax+a2)
| x |
∴f′(x)=
| ||
| 2x |
令f′(x)=0.解得x=
| a |
| 10 |
| a |
| 2 |
当f′(x)>0时,x在(0,
| a |
| 10 |
| a |
| 2 |
当f′(x)<0时,x在(
| a |
| 10 |
| a |
| 2 |
①当
| a |
| 10 |
由f(1)=8,解得a=2±2
| 2 |
②当
| a |
| 2 |
由f(1)=8,解得a=2±2
| 2 |
③当
| a |
| 10 |
| a |
| 2 |
由f(4)=8,解得a=10,
④当1<
| a |
| 10 |
解得,a=2±2
| 2 |
⑤当1<
| a |
| 2 |
| a |
| 2 |
综上所述,a=10.
点评:本题考查的是导数知识,重点是利用导数判断函数的单调性,难点是分类讨论.对学生的能力要求较高,属于难题.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
阅读如图所示的程序框图,则该算法的功能是( )
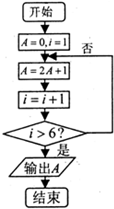

| A、计算数列{2n-1}前5项的和 |
| B、计算数列{2n-1}前5项的和 |
| C、计算数列{2n-1}前6项的和 |
| D、计算数列{2n-1}前6项的和 |
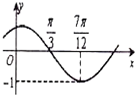 函数f(x)=sin(ωx+φ)(ω>0,|φ|<
函数f(x)=sin(ωx+φ)(ω>0,|φ|<| π |
| 2 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
在平面直角坐标系中,直线(
-
)x+y=3和直线x+(
-
)y=2的位置关系是( )
| 3 |
| 2 |
| 2 |
| 3 |
| A、相互但不垂直 | B、平行 |
| C、垂直 | D、重合 |
不论实数k取何值时,直线(k+1)x+(1-3k)y+2k-2=0恒过一定点,则该点的坐标是D( )
| A、(1,4) |
| B、(2,1) |
| C、(3,1) |
| D、(1,1) |
若函数f(x)(x∈R)是奇函数,则( )
| A、函数f (x2)是奇函数 |
| B、函数[f (x)]2是奇函数 |
| C、函数f (x)•x2是奇函数 |
| D、函数f(x)+x2是奇函数 |