题目内容
7位同学站成一排,按下列要求,各有多少不同排法,
(1)甲站在某一固定位置;
(2)甲站中间,乙与甲相邻;
(3)甲、乙相邻;
(4)甲、乙两人不相邻;
(5)甲、乙、丙三人相邻;
(6)甲、乙、丙三人中任何两人都不相邻.
(1)甲站在某一固定位置;
(2)甲站中间,乙与甲相邻;
(3)甲、乙相邻;
(4)甲、乙两人不相邻;
(5)甲、乙、丙三人相邻;
(6)甲、乙、丙三人中任何两人都不相邻.
考点:计数原理的应用
专题:计算题,排列组合
分析:对这几个事件不同排法和数的计算,根据分步原理与分类原理直接计算即可.
解答:
解:(1)甲站在某一固定位置,有
种不同排法;
(2)甲站中间,乙与甲相邻,有
种不同排法;
(3)甲、乙相邻,有
种不同排法;
(4)甲、乙两人不相邻,有
-
种不同排法;
(5)甲、乙、丙三人相邻,有
种不同排法;
(6)甲、乙、丙三人中任何两人都不相邻,有
种不同排法.
| A | 6 6 |
(2)甲站中间,乙与甲相邻,有
| C | 1 2 |
| A | 5 5 |
(3)甲、乙相邻,有
| A | 6 6 |
| A | 2 2 |
(4)甲、乙两人不相邻,有
| A | 7 7 |
| A | 6 6 |
| A | 2 2 |
(5)甲、乙、丙三人相邻,有
| A | 5 5 |
| A | 3 3 |
(6)甲、乙、丙三人中任何两人都不相邻,有
| A | 4 4 |
| A | 3 5 |
点评:本题考查排列、组合及简单计数问题,本题在计数时根据具体情况选用了插空法、捆绑法等方法,做题时要注意体会这些方法的原理及其实际意义.

练习册系列答案
相关题目
已知数列{an}满足:a1=1,an=
+
(n≥2),分别求出S1,S2,S3,S4,通过归纳猜想得到Sn=( )
| Sn |
| Sn-1 |
| A、2n-1 |
| B、n2 |
| C、n |
| D、2n |
下列说法错误的是( )
| A、命题“?x∈R,x2-2x=0”的否定是“?x∈R,x2-2x≠0” |
| B、命题“若m>0,则方程x2+x-m=0有实根”的逆否命题为真命题 |
| C、若命题“p∧q”为真命题,则“p∨q”为真命题 |
| D、“x>1”是“|x|>0”的必要不充分条件 |
设f(x)=
,则f(2015)=( )
|
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|
已知a=(
)
,b=log6
,c=log
,则a,b,c的大小关系是( )
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 3 |
| A、a>b>c |
| B、c>a>b |
| C、a>c>b |
| D、c>b>a |
阅读如图所示的程序框图,则该算法的功能是( )
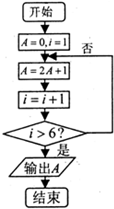

| A、计算数列{2n-1}前5项的和 |
| B、计算数列{2n-1}前5项的和 |
| C、计算数列{2n-1}前6项的和 |
| D、计算数列{2n-1}前6项的和 |