题目内容
已知全集U=R，A={x|x≤0}，B={x|x＞-1}，则集合∁U（A∩B）=（ ）
| A、{x|-1＜x≤0} |
| B、{x|-1≤x≤0} |
| C、{x|x≤-1或x≥0} |
| D、{x|x≤-1或x＞0} |
考点：交、并、补集的混合运算
专题：集合
分析：根据集合的基本运算进行求解即可．
解答：
解：∵A={x|x≤0}，B={x|x＞-1}，
∴A∩B={x|-1＜x≤0}，
则∁U（A∩B）={x|x≤-1或x＞0}，
故选：D．
∴A∩B={x|-1＜x≤0}，
则∁U（A∩B）={x|x≤-1或x＞0}，
故选：D．
点评：本题主要考查集合关系的应用，比较基础．
练习册系列答案
相关题目
阅读如图所示的程序框图，则该算法的功能是（ ）
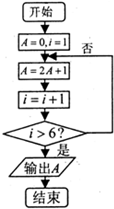
| A、计算数列{2n-1}前5项的和 |
| B、计算数列{2n-1}前5项的和 |
| C、计算数列{2n-1}前6项的和 |
| D、计算数列{2n-1}前6项的和 |
不论实数k取何值时，直线（k+1）x+（1-3k）y+2k-2=0恒过一定点，则该点的坐标是D（ ）
| A、（1，4） |
| B、（2，1） |
| C、（3，1） |
| D、（1，1） |
若函数f（x）（x∈R）是奇函数，则（ ）
| A、函数f （x2）是奇函数 |
| B、函数[f （x）]2是奇函数 |
| C、函数f （x）•x2是奇函数 |
| D、函数f（x）+x2是奇函数 |
已知抛物线y2=8x的焦点F到双曲线C：
-
=1（a＞0，b＞0）渐近线的距离为
，点P是抛物线y2=8x上的一动点，P到双曲线C的上焦点F1（0，c）的距离与到直线x=-2的距离之和的最小值为3，则该双曲线的方程为（ ）
| y2 |
| a2 |
| x2 |
| b2 |
4
| ||
| 5 |
A、
| ||||
B、
| ||||
C、y2-
| ||||
D、
|