题目内容
已知函数f(x)=
.
(Ⅰ)若a=-1,证明:函数f(x)是(0,+∞)上的减函数;
(Ⅱ)若曲线y=f(x)在点(1,f(1))处的切线与直线x-y=0平行,求a的值;
(Ⅲ)若x>0,证明:
>
(其中e=2.71828…是自然对数的底数).
| ln(x-a) |
| x |
(Ⅰ)若a=-1,证明:函数f(x)是(0,+∞)上的减函数;
(Ⅱ)若曲线y=f(x)在点(1,f(1))处的切线与直线x-y=0平行,求a的值;
(Ⅲ)若x>0,证明:
| ln(x+1) |
| x |
| x |
| ex-1 |
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(Ⅰ) 先求导,得到f′(x)=
,再构造函数g(x)=x-(x+1)ln(x+1),求出g(x)的最大值为0,继而得到f′(x)≤0在(0,+∞)上恒成立,问题得以证明;
(Ⅱ)欲求a的值,根据在点(1,f(1))处的切线方程,只须求出其斜率的值即可,故先利用导数求出在x=1处的导函数值,再结合导数的几何意义即可求出切线的斜率,解方程即可得;
(Ⅲ)
>
=
,由(Ⅰ)的结论,故要证原不等式成立,只需要证明:当x>0时,x<ex-1,构造函数,利用导数和函数的最值的关系即可证明.
| x-(x+1)ln(x+1) |
| (x+1)x2 |
(Ⅱ)欲求a的值,根据在点(1,f(1))处的切线方程,只须求出其斜率的值即可,故先利用导数求出在x=1处的导函数值,再结合导数的几何意义即可求出切线的斜率,解方程即可得;
(Ⅲ)
| ln(x+1) |
| x |
| x |
| ex-1 |
| ln(ex-1+1) |
| ex-1 |
解答:
解:(Ⅰ)当a=-1时,f(x)=
,
∴函数的定义域为(-1,0)∪(0,+∞),
∴f′(x)=
,
设g(x)=x-(x+1)ln(x+1),
∴g′(x)=1-[ln(x+1)+1]=-ln(x+1),
∴g′(x)≤0在(0,+∞)上恒成立,
∴g(x)在(0,+∞)上为减函数,
∴g(x)≤g(0)=0,
∴f′(x)≤0在(0,+∞)上恒成立,
∴f(x)在(0,+∞)上为减函数.
(Ⅱ)∵f′(x)=
,
∴k=f′(1)=
,
∵y=f(x)在点(1,f(1))处的切线与直线x-y=0平行
∴
=1,
即ln(1-a)=
,分别画出y=ln(1-x)与y=
的图象,
又图象可知交点为(0,0)
∴解得a=0.
(Ⅲ):∵
=
=
,
∴
>
=
,
由(Ⅰ)知,当a=-1时,f(x)=
在(0,+∞)上为减函数,
故要证原不等式成立,只需要证明:当x>0时,x<ex-1,
令h(x)=ex-1-x,
则h′(x)=ex-1>0,
∴h(x)在(0,+∞)上为增函数,
∴h(x)>h(0)=0,即x<ex-1,
∴f(x)>f(ex-1)
即
>
.
| ln(x+1) |
| x |
∴函数的定义域为(-1,0)∪(0,+∞),
∴f′(x)=
| x-(x+1)ln(x+1) |
| (x+1)x2 |
设g(x)=x-(x+1)ln(x+1),
∴g′(x)=1-[ln(x+1)+1]=-ln(x+1),
∴g′(x)≤0在(0,+∞)上恒成立,
∴g(x)在(0,+∞)上为减函数,
∴g(x)≤g(0)=0,
∴f′(x)≤0在(0,+∞)上恒成立,

∴f(x)在(0,+∞)上为减函数.
(Ⅱ)∵f′(x)=
| x-(x-a)ln(x-a) |
| (x-a)x2 |
∴k=f′(1)=
| 1-(1-a)ln(1-a) |
| 1-a |
∵y=f(x)在点(1,f(1))处的切线与直线x-y=0平行
∴
| 1-(1-a)ln(1-a) |
| 1-a |
即ln(1-a)=
| a |
| 1-a |
| x |
| 1-x |
又图象可知交点为(0,0)
∴解得a=0.
(Ⅲ):∵
| x |
| ex-1 |
| lnex |
| ex-1 |
| ln(ex-1+1) |
| ex-1 |
∴
| ln(x+1) |
| x |
| x |
| ex-1 |
| ln(ex-1+1) |
| ex-1 |
由(Ⅰ)知,当a=-1时,f(x)=
| ln(x+1) |
| x |
故要证原不等式成立,只需要证明:当x>0时,x<ex-1,
令h(x)=ex-1-x,
则h′(x)=ex-1>0,
∴h(x)在(0,+∞)上为增函数,
∴h(x)>h(0)=0,即x<ex-1,
∴f(x)>f(ex-1)
即
| ln(x+1) |
| x |
| x |
| ex-1 |
点评:本题考查导数和函数的单调性最值的关系,以及导数的几何意义,考查了不等式的证明问题,培养了学生的转化能力,运算能力,处理问题的能力,属于难题

练习册系列答案
相关题目
下列说法错误的是( )
| A、命题“?x∈R,x2-2x=0”的否定是“?x∈R,x2-2x≠0” |
| B、命题“若m>0,则方程x2+x-m=0有实根”的逆否命题为真命题 |
| C、若命题“p∧q”为真命题,则“p∨q”为真命题 |
| D、“x>1”是“|x|>0”的必要不充分条件 |
已知a=(
)
,b=log6
,c=log
,则a,b,c的大小关系是( )
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 3 |
| A、a>b>c |
| B、c>a>b |
| C、a>c>b |
| D、c>b>a |
阅读如图所示的程序框图,则该算法的功能是( )
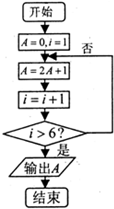

| A、计算数列{2n-1}前5项的和 |
| B、计算数列{2n-1}前5项的和 |
| C、计算数列{2n-1}前6项的和 |
| D、计算数列{2n-1}前6项的和 |
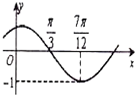 函数f(x)=sin(ωx+φ)(ω>0,|φ|<
函数f(x)=sin(ωx+φ)(ω>0,|φ|<| π |
| 2 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
在平面直角坐标系中,直线(
-
)x+y=3和直线x+(
-
)y=2的位置关系是( )
| 3 |
| 2 |
| 2 |
| 3 |
| A、相互但不垂直 | B、平行 |
| C、垂直 | D、重合 |