题目内容
某市各级各类中小学每年都要进行“学生体质健康测试”,测试成绩满分为100分,规定测试成绩在[85,100]之间为体质优秀;在[75,85)之间为体质良好;在[60,75)之间为体质合格;在[0,60)之间为体质不合格.现从某校高三年级的300名学生中随机抽取30名学生体质健康测试成绩,其茎叶图如图所示:

(Ⅰ)估计该校学生中体质为良好和优秀的人数有多少?
(Ⅱ)根据以上30名学生体质健康测试成绩,现采用分层抽样的方法,从体质为优秀和良好的学生中抽取5名学生,再从这5名学生中选出3人.求在选出3名学生中至少有1名体质为优秀的概率.

(Ⅰ)估计该校学生中体质为良好和优秀的人数有多少?
(Ⅱ)根据以上30名学生体质健康测试成绩,现采用分层抽样的方法,从体质为优秀和良好的学生中抽取5名学生,再从这5名学生中选出3人.求在选出3名学生中至少有1名体质为优秀的概率.
考点:古典概型及其概率计算公式,分层抽样方法,茎叶图
专题:概率与统计
分析:(Ⅰ)根据抽样的定义和条件即可估计该校体质为良好和优秀的学生人数;
(Ⅱ)求出随机变量的分布列以及数学期望公式进行计算即可.
(Ⅱ)求出随机变量的分布列以及数学期望公式进行计算即可.
解答:
解:(Ⅰ)根据抽样的性质,
估计该校学生中体质为良好的学生人数有:
×300=150人,
该校学生中体质为优秀的学生人数有:
×300=100人.
(Ⅱ)依题意,体质为良好和优秀的学生人数之比为 15:10=3:2.
所以,从体质为良好的学生中抽取的人数为
×5=3人,
从体质为优秀的学生中抽取的人数为
×5=2人,
设“在选出的3名学生中至少有名体质为优秀”为事件A,
则 P(A)=1-
=
.
故在选出的3名学生中至少有名体质为优秀的概率为
.
估计该校学生中体质为良好的学生人数有:
| 15 |
| 30 |
该校学生中体质为优秀的学生人数有:
| 10 |
| 30 |
(Ⅱ)依题意,体质为良好和优秀的学生人数之比为 15:10=3:2.
所以,从体质为良好的学生中抽取的人数为
| 3 |
| 5 |
从体质为优秀的学生中抽取的人数为
| 2 |
| 5 |
设“在选出的3名学生中至少有名体质为优秀”为事件A,
则 P(A)=1-
| ||
|
| 9 |
| 10 |
故在选出的3名学生中至少有名体质为优秀的概率为
| 9 |
| 10 |
点评:本题主要考查茎叶图的应用以及古典概型概率的计算,考查学生的计算能力.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
曲线y=4x-x3在点(-1,-3)处切线的斜率为( )
| A、7 | B、-7 | C、1 | D、-1 |
已知f1(x)=sinx+cosx,fn+1(x)是fn(x)的导函数,即f2(x)=f1′(x),f3(x)=f2′(x),…,fn+1(x)=fn′(x),n∈N*,则f2014(x)等于( )
| A、-sinx-cosx |
| B、sinx-cosx |
| C、sinx+cosx |
| D、-sinx+cosx |
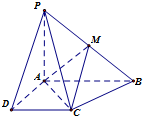 已知四棱锥P-ABCD的底面为直角梯形,AB∥CD,∠DAB=
已知四棱锥P-ABCD的底面为直角梯形,AB∥CD,∠DAB=