题目内容
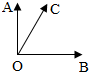如图所示：|| OA |
| OB |
| 3 |
| OA |
| OB |
| π |
| 6 |
| OC |
| OA |
| OB |
| λ |
| μ |
A、
| ||||
B、
| ||||
| C、3 | ||||
D、
|
考点：数量积表示两个向量的夹角,平面向量的基本定理及其意义
专题：平面向量及应用
分析：由题设条件，可由数量积公式及∠AOC=
建立关于两参数λ、μ的等式解出两者的关系
| π |
| 6 |
解答：
解：由题意，|
|=2，
=2
，且
•
=0，∠AOC=
，
∴
2=λ2
2+λμ
•
+μ2
2=4λ2+12μ2
∴cos∠AOC=
，即
=
=
，
整理得9μ2=λ2，又由的给图象可得，λ、μ皆为正数，
解得
=3，
故选：C．
| OA |
| OB |
| 3 |
| OA |
| OB |
| π |
| 6 |
∴
| OC |
| OA |
| OA |
| OB |
| OB |
∴cos∠AOC=
| ||||
|
|
| ||
| 2 |
λ
| ||
2
|
| 4λ | ||
2
|
整理得9μ2=λ2，又由的给图象可得，λ、μ皆为正数，
解得
| λ |
| μ |
故选：C．
点评：本题考查平面向量的数量积公式及两向量垂直的表示，考查了方程的思想及推理计算的能力
练习册系列答案
相关题目
已知函数f（x）=
，x∈[2，4]对于满足2＜x1＜x2＜4的任意x1，x2，给出下列结论：
①x1f（x2）＞x2f（x1）
②x2f（x1）＞x1f（x2）
③（x2-x1）[f（x2）-f（x1）]＜0
④（x2-x1）[f（x2）-f（x1）]＞0
其中正确的是（ ）
| 4-(x-2)2 |
①x1f（x2）＞x2f（x1）
②x2f（x1）＞x1f（x2）
③（x2-x1）[f（x2）-f（x1）]＜0
④（x2-x1）[f（x2）-f（x1）]＞0
其中正确的是（ ）
| A、①③ | B、①④ | C、②③ | D、②④ |
曲线y=4x-x3在点（-1，-3）处切线的斜率为（ ）
| A、7 | B、-7 | C、1 | D、-1 |
若不等式mx2+mnx+n＞0的解集为{x|1＜x＜2}，则m+n的值为（ ）
A、
| ||
B、
| ||
C、-
| ||
D、-
|
复数
（i为虚数单位）为纯虚数，则实数m的值为（ ）
| m-i |
| 2+3i |
A、
| ||
B、
| ||
C、
| ||
D、
|
设z=1-i（i是虚数单位），则复数
+i2的实部是（ ）
| 3 |
| z |
A、
| ||||
B、
| ||||
C、-
| ||||
D、
|
已知f1（x）=sinx+cosx，fn+1（x）是fn（x）的导函数，即f2（x）=f1′（x），f3（x）=f2′（x），…，fn+1（x）=fn′（x），n∈N*，则f2014（x）等于（ ）
| A、-sinx-cosx |
| B、sinx-cosx |
| C、sinx+cosx |
| D、-sinx+cosx |
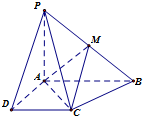已知四棱锥P-ABCD的底面为直角梯形，AB∥CD，∠DAB=