题目内容
已知△ABC的三个内角A,B,C满足:sin2(A+C)=
sinBcosB,cos﹙C-A﹚=-2cos2A.
(1)试判断△ABC的形状;
(2)已知函数f(x)=sinx-
cosx(x∈R),求f(A+
)的值.
| 3 |
(1)试判断△ABC的形状;
(2)已知函数f(x)=sinx-
| 3 |
| π |
| 4 |
考点:三角函数中的恒等变换应用,两角和与差的正弦函数
专题:三角函数的图像与性质
分析:(1)首先,根据所给条件,A+C=π-B,分别利用已知条件,得到A=B=
,从而得到三角形的形状.
(2)借助于辅助角公式,利用三角函数公式和两角和与差的三角公式进行化简求值即可.
| π |
| 3 |
(2)借助于辅助角公式,利用三角函数公式和两角和与差的三角公式进行化简求值即可.
解答:
解:(1)∵A+C=π-B,
∴sin2B=
sinBcosB,
∴tanB=
,∵0<B<π,
∴B=
,
∴C=
-A,
∵cos﹙C-A﹚=-2cos2A,
∴cos(2A-
)=-2cos2A,
∴cos2Acos
+sin2Asin
=-2cos2A,
∴
sin2A+
cos2A=0,
∴
sin(2A+
)=0,
∴2A+
=π,
∴A=
,
∴△ABC的形状为等边三角形;
(2)∵函数f(x)=sinx-
cosx(x∈R)
=2sin(x-
),
∴f(A+
)=2sin(
+
-
)
=2sin
=
∴f(A+
)的值为
.
∴sin2B=
| 3 |
∴tanB=
| 3 |
∴B=
| π |
| 3 |
∴C=
| 2π |
| 3 |
∵cos﹙C-A﹚=-2cos2A,
∴cos(2A-
| 2π |
| 3 |
∴cos2Acos
| 2π |
| 3 |
| 2π |
| 3 |
∴
| ||
| 2 |
| 3 |
| 2 |
∴
| 3 |
| π |
| 3 |
∴2A+
| π |
| 3 |
∴A=
| π |
| 3 |
∴△ABC的形状为等边三角形;
(2)∵函数f(x)=sinx-
| 3 |
=2sin(x-
| π |
| 3 |
∴f(A+
| π |
| 4 |
| π |
| 3 |
| π |
| 4 |
| π |
| 3 |
=2sin
| π |
| 4 |
| 2 |
∴f(A+
| π |
| 4 |
| 2 |
点评:本题重点考查三角函数及其恒等变换公式的灵活运用,注意三角形中的边角关系问题,属于中档题.

练习册系列答案
相关题目
复数
(i为虚数单位)为纯虚数,则实数m的值为( )
| m-i |
| 2+3i |
A、
| ||
B、
| ||
C、
| ||
D、
|
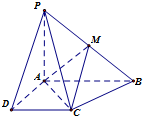 已知四棱锥P-ABCD的底面为直角梯形,AB∥CD,∠DAB=
已知四棱锥P-ABCD的底面为直角梯形,AB∥CD,∠DAB=