题目内容
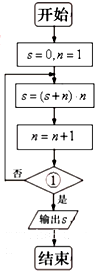
如图是某算法的程序框图,则程序运行后输出的结果是124,则判断框①处应填入的条件是( )

| A、n>2 | B、n>3 |
| C、n>4 | D、n>5 |
考点:程序框图
专题:算法和程序框图
分析:分别计算n=1,2,3,…时的s的值,直到满足S=124时,进而即可得出判定框①中的条件.
解答:
解答:解:由s=0,n=1得出s=(0+1)×1=1,n=2;
由s=1,n=2得出s=(1+2)×2=6;
由s=6,n=3得出s=(6+3)×3=27.
由s=27,n=4得出s=(27+4)×4=124,n=5,此时不满足条件为输出结果,应终止循环,
因此判定框①中应为n>4.
故选C.
由s=1,n=2得出s=(1+2)×2=6;
由s=6,n=3得出s=(6+3)×3=27.
由s=27,n=4得出s=(27+4)×4=124,n=5,此时不满足条件为输出结果,应终止循环,
因此判定框①中应为n>4.
故选C.
点评:点评:本题主要考查程序框图的识别和应用,正确理解循环结构和判断框的功能是解题的关键.

练习册系列答案
相关题目
已知f(x)是定义在[-1,1]上的奇函数,当x1≤x2时,f(x1)≤f(x2).当x∈[0,1]时,2f(
)=f(x),f(x)=1-f(1-x),则f(-
)+f(-
)+…+f(-
)+f(-
)=( )
| x |
| 5 |
| 150 |
| 2014 |
| 151 |
| 2014 |
| 170 |
| 2014 |
| 171 |
| 2014 |
A、-
| ||
| B、-5 | ||
| C、-6 | ||
D、-
|
设集合U={1,2,3,4,5},A={2,3,5},则∁UA=( )
| A、{5} |
| B、{1,4} |
| C、{2,3} |
| D、{2,3,5} |
设双曲线的中心为原点O,焦点在x轴上,两条渐近线分别为l1,l2,经过右焦点F且垂直于l1的直线分别交l1,l2于A,B两点,已知
与
同向,且丨
丨是丨
丨,丨
丨的等差中项,则l1,l2的方程是( )
| BF |
| FA |
| AB |
| OA |
| OB |
A、y=±
| ||
| B、y=±2x | ||
C、y=±
| ||
D、y=±
|
下列各式中,函数的个数是( )
①y=1;②y=x2;③y=1-x;④y=
+
.
①y=1;②y=x2;③y=1-x;④y=
| x-2 |
| 1-x |
| A、4 | B、3 | C、2 | D、1 |