题目内容
已知等比数列{an}的首项为2,公比为3,前n项和为Sn,若log3[
an•(S4m+1)]=9,则
+
的最小值是 .
| 1 |
| 2 |
| 1 |
| n |
| 4 |
| m |
考点:等比数列的性质
专题:综合题,等差数列与等比数列,不等式的解法及应用
分析:根据等比数列{an}的首项为2,公比为3,前n项和为Sn,可得an=2•3n-1;Sn=3n-1,由log3[
an•(S4m+1)]=9,可得n+4m=10,进而利用“1”的代换,结合基本不等式,即可得出结论.
| 1 |
| 2 |
解答:
解:∵等比数列{an}的首项为2,公比为3,前n项和为Sn,
∴an=2•3n-1;Sn=3n-1,
∵log3[
an•(S4m+1)]=9,
∴(n-1)+4m=9,
∴n+4m=10,
∴
+
=
(n+4m)(
+
)=
(17+
+
)≥
(17+8)=2.5
当且仅当m=n=2时取等号,
∴
+
的最小值是2.5.
故答案为:2.5.
∴an=2•3n-1;Sn=3n-1,
∵log3[
| 1 |
| 2 |
∴(n-1)+4m=9,
∴n+4m=10,
∴
| 1 |
| n |
| 4 |
| m |
| 1 |
| 10 |
| 1 |
| n |
| 4 |
| m |
| 1 |
| 10 |
| 4n |
| m |
| 4m |
| n |
| 1 |
| 10 |
当且仅当m=n=2时取等号,
∴
| 1 |
| n |
| 4 |
| m |
故答案为:2.5.
点评:本题考查等比数列的通项与性质,考查对数运算,考查基本不等式,确定n+4m=10,进而利用“1”的代换,结合基本不等式是关键.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
下列说法正确的是( )
| A、若“p∧q”为假命题,则p,q均为假命题 |
| B、“x>2”是“x2-3x+2>0”的必要不充分条件 |
| C、命题“?x∈R使得x2+x+1<0”的否定是:“?x∈R 均有x2+x+1<0” |
| D、在△ABC中,若A是最大角,则“sin2B+sin2C<sin2A”是“△ABC为钝角三角形”的充要条件 |
如图是某算法的程序框图,则程序运行后输出的结果是124,则判断框①处应填入的条件是( )
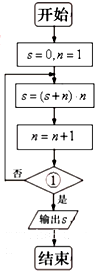

| A、n>2 | B、n>3 |
| C、n>4 | D、n>5 |