题目内容
下列各式中，函数的个数是（ ）
①y=1；②y=x2；③y=1-x；④y=
+
．
①y=1；②y=x2；③y=1-x；④y=
| x-2 |
| 1-x |
| A、4 | B、3 | C、2 | D、1 |
考点：函数的概念及其构成要素
专题：函数的性质及应用
分析：根据函数的定义方便继续判断即可．
解答：
解：根据函数的定义可知，①y=1；②y=x2；③y=1-x；都是函数，
对应④，要使函数有意义，则
，
即
，则x无解，∴④不是函数．
故选：B．
对应④，要使函数有意义，则
|
即
|
故选：B．
点评：本题主要考查函数的判断，根据函数的定义是解决本题的关键，比较基础．
练习册系列答案
走进文言文系列答案
相关题目
下列说法正确的是（ ）
| A、若“p∧q”为假命题，则p，q均为假命题 |
| B、“x＞2”是“x2-3x+2＞0”的必要不充分条件 |
| C、命题“?x∈R使得x2+x+1＜0”的否定是：“?x∈R 均有x2+x+1＜0” |
| D、在△ABC中，若A是最大角，则“sin2B+sin2C＜sin2A”是“△ABC为钝角三角形”的充要条件 |
如图是某算法的程序框图，则程序运行后输出的结果是124，则判断框①处应填入的条件是（ ）
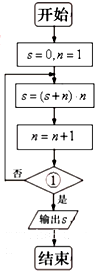
| A、n＞2 | B、n＞3 |
| C、n＞4 | D、n＞5 |
（ax+
）（2x-1）5的展开式中各项系数的和为2，则该展开式中常数项为（ ）
| 1 |
| x |
| A、-20 | B、-10 |
| C、10 | D、20 |
在平面直角坐标系xOy中，已知B（1，0），∠AOB=120°，|