题目内容
讨论直线l1:ax+8y-a-4=0与直线l2:x+2ay-2a+1=0的位置关系.
考点:直线的一般式方程与直线的平行关系,直线的一般式方程与直线的垂直关系
专题:直线与圆
分析:分①当a=0时、②当a≠0时两种情况,分别讨论两直线的位置关系,属于基础题.
解答:
解:①当a=0时,直线l1:8y-4=0,直线l2:x+1=0,两直线垂直.
②当a≠0时,两直线的斜率分别为-
,-
,
若-
=-
,求得a=±2,
当a=2,直线l1:x+4y-3=0,直线l2:x+4y-3=0,两直线重合;
当a=-2,直线l1:x-4y+1=0,直线l2:x-4y+5=0,两直线平行.
若-
≠-
,求得a≠±2,此时,两直线相交.
②当a≠0时,两直线的斜率分别为-
| a |
| 8 |
| 1 |
| 2a |
若-
| a |
| 8 |
| 1 |
| 2a |
当a=2,直线l1:x+4y-3=0,直线l2:x+4y-3=0,两直线重合;
当a=-2,直线l1:x-4y+1=0,直线l2:x-4y+5=0,两直线平行.
若-
| a |
| 8 |
| 1 |
| 2a |
点评:本题主要考查两条直线平行、垂直、相交的判定方法,属于基础题.

练习册系列答案
相关题目
如图是某算法的程序框图,则程序运行后输出的结果是124,则判断框①处应填入的条件是( )
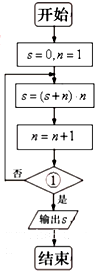

| A、n>2 | B、n>3 |
| C、n>4 | D、n>5 |
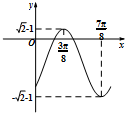 已知函数f(x)=asin(ωx+θ)-b的部分图象如图,其中ω>0,|θ|<
已知函数f(x)=asin(ωx+θ)-b的部分图象如图,其中ω>0,|θ|<