题目内容
已知f(x)是定义在[-1,1]上的奇函数,当x1≤x2时,f(x1)≤f(x2).当x∈[0,1]时,2f(
)=f(x),f(x)=1-f(1-x),则f(-
)+f(-
)+…+f(-
)+f(-
)=( )
| x |
| 5 |
| 150 |
| 2014 |
| 151 |
| 2014 |
| 170 |
| 2014 |
| 171 |
| 2014 |
A、-
| ||
| B、-5 | ||
| C、-6 | ||
D、-
|
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:首先,结合f(x)=1-f(1-x),先求解f(0) ,f(1) ,f(
)的值,然后,利用2f(
)=f(x),找规律,最后,利用函数为奇函数进行求解.
| 1 |
| 2 |
| x |
| 5 |
解答:
解:∵f(x)为奇函数,
∴f(0)=0,根据f(x)=1-f(1-x),
∴f(1)=1 ,f(
)=
,
∵2f(
)=f(x),
∴f(
)=
f(1)=
,
∵2f(
)=f(
)=
,
∴f(
)=
,
∵2f(
)=f(
)=
,
∴f(
)=
,
∵
<
<
,且函数f(x)当x1≤x2时,f(x1)≤f(x2).
∴
=f(
)≤f(
)≤f(
)=
,
同理,
f(
)=f(
)=…=f(
)=
,
∴原式=-[f(
)+f(
)+…+f(
)
=-
=-
,
故选:A.
∴f(0)=0,根据f(x)=1-f(1-x),
∴f(1)=1 ,f(
| 1 |
| 2 |
| 1 |
| 2 |
∵2f(
| x |
| 5 |
∴f(
| 1 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
∵2f(
| 1 |
| 25 |
| 1 |
| 5 |
| 1 |
| 2 |
∴f(
| 1 |
| 25 |
| 1 |
| 4 |
∵2f(
| 1 |
| 10 |
| 1 |
| 2 |
| 1 |
| 2 |
∴f(
| 1 |
| 10 |
| 1 |
| 4 |
∵
| 1 |
| 25 |
| 150 |
| 2014 |
| 1 |
| 10 |
∴
| 1 |
| 4 |
| 1 |
| 25 |
| 150 |
| 2014 |
| 1 |
| 10 |
| 1 |
| 4 |
同理,
f(
| 151 |
| 2014 |
| 152 |
| 2014 |
| 171 |
| 2014 |
| 1 |
| 4 |
∴原式=-[f(
| 151 |
| 2014 |
| 152 |
| 2014 |
| 171 |
| 2014 |
=-
| 22 |
| 4 |
| 11 |
| 2 |
故选:A.
点评:本题重点考查函数的基本性质及其灵活运用,注意单调性和奇偶性的综合运用,属于中档题.

练习册系列答案
相关题目
下列说法正确的是( )
| A、若“p∧q”为假命题,则p,q均为假命题 |
| B、“x>2”是“x2-3x+2>0”的必要不充分条件 |
| C、命题“?x∈R使得x2+x+1<0”的否定是:“?x∈R 均有x2+x+1<0” |
| D、在△ABC中,若A是最大角,则“sin2B+sin2C<sin2A”是“△ABC为钝角三角形”的充要条件 |
五名男生与两名女生排成一排照相,如果男生甲必须站在正中间,两名女生必须相邻,符合条件的排法共有( )
| A、48种 | B、192种 |
| C、240种 | D、288种 |
如图是某算法的程序框图,则程序运行后输出的结果是124,则判断框①处应填入的条件是( )
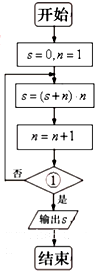

| A、n>2 | B、n>3 |
| C、n>4 | D、n>5 |
 在平面直角坐标系xOy中,已知B(1,0),∠AOB=120°,|
在平面直角坐标系xOy中,已知B(1,0),∠AOB=120°,|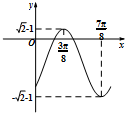 已知函数f(x)=asin(ωx+θ)-b的部分图象如图,其中ω>0,|θ|<
已知函数f(x)=asin(ωx+θ)-b的部分图象如图,其中ω>0,|θ|<