题目内容
解方程：3x+4x+5x=6x．
考点：指数函数的图像与性质
专题：函数的性质及应用
分析：在方程的两边同除以6x，可得(
)x+(
)x+(
)x=1，构造函数F（x）=(
)x+(
)x+(
)x-1，可得其为减函数，经验证x=3是函数F（x）的零点，可得结论．
| 1 |
| 2 |
| 2 |
| 3 |
| 5 |
| 6 |
| 1 |
| 2 |
| 2 |
| 3 |
| 5 |
| 6 |
解答：
解：在方程的两边同除以6x，可得(
)x+(
)x+(
)x=1，
∵指数函数y=(
)x，y=(
)x，y=(
)x均为减函数，
∴F（x）=(
)x+(
)x+(
)x-1为减函数，
经验证x=3是函数F（x）的零点，且是唯一的零点，
∴原方程有唯一的解x=3
| 1 |
| 2 |
| 2 |
| 3 |
| 5 |
| 6 |
∵指数函数y=(
| 1 |
| 2 |
| 2 |
| 3 |
| 5 |
| 6 |
∴F（x）=(
| 1 |
| 2 |
| 2 |
| 3 |
| 5 |
| 6 |
经验证x=3是函数F（x）的零点，且是唯一的零点，
∴原方程有唯一的解x=3
点评：本题考查指数函数的性质，得出函数F（x）单调递减是解决问题的关键，属基础题．
练习册系列答案
优生乐园系列答案
新编小学单元自测题系列答案
相关题目
如图是某算法的程序框图，则程序运行后输出的结果是124，则判断框①处应填入的条件是（ ）
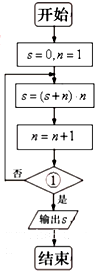
| A、n＞2 | B、n＞3 |
| C、n＞4 | D、n＞5 |
在平面直角坐标系xOy中，已知B（1，0），∠AOB=120°，|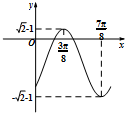
已知函数f（x）=asin（ωx+θ）-b的部分图象如图，其中ω＞0，|θ|＜