题目内容
设双曲线的中心为原点O,焦点在x轴上,两条渐近线分别为l1,l2,经过右焦点F且垂直于l1的直线分别交l1,l2于A,B两点,已知
与
同向,且丨
丨是丨
丨,丨
丨的等差中项,则l1,l2的方程是( )
| BF |
| FA |
| AB |
| OA |
| OB |
A、y=±
| ||
| B、y=±2x | ||
C、y=±
| ||
D、y=±
|
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:由勾股定理得出直角三角形的2个直角边的长度比,联想到渐近线的夹角,求出渐近线的斜率,即可求出直线方程.
解答:
解:设双曲线
-
=1(a>0,b>0),
∵丨
丨是丨
丨,丨
丨的等差中项,
∴2|AB|=|OB|+|OA|,
∵|AB|2=(|OB|-|OA|)(|OB|+|OA|)=(|OB|-|OA|)2|AB|
∴|AB|=2(|OB|-|OA|),
∵2|AB|=|OB|+|OA|
∴|OA|=
|AB|,
∴tan∠AOB=
而由对称性可知:设OB的斜率为k,∴
=
,
∴2k2+3k-2=0,∴k=
(k=-2舍去).
∴l1,l2的方程是y=±
x.
故选:A.
| x2 |
| a2 |
| y2 |
| b2 |
∵丨
| AB |
| OA |
| OB |
∴2|AB|=|OB|+|OA|,
∵|AB|2=(|OB|-|OA|)(|OB|+|OA|)=(|OB|-|OA|)2|AB|
∴|AB|=2(|OB|-|OA|),
∵2|AB|=|OB|+|OA|
∴|OA|=
| 3 |
| 4 |
∴tan∠AOB=
| 4 |
| 3 |
而由对称性可知:设OB的斜率为k,∴
| 2k |
| 1-k2 |
| 4 |
| 3 |
∴2k2+3k-2=0,∴k=
| 1 |
| 2 |
∴l1,l2的方程是y=±
| 1 |
| 2 |
故选:A.
点评:本题考查了双曲线的简单性质以及等差数列的性质,由|OA|=
|AB|,联想到对应的是渐近线的夹角的正切值,是解题的关键.
| 3 |
| 4 |

练习册系列答案
相关题目
五名男生与两名女生排成一排照相,如果男生甲必须站在正中间,两名女生必须相邻,符合条件的排法共有( )
| A、48种 | B、192种 |
| C、240种 | D、288种 |
如图是某算法的程序框图,则程序运行后输出的结果是124,则判断框①处应填入的条件是( )
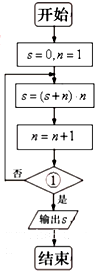

| A、n>2 | B、n>3 |
| C、n>4 | D、n>5 |
如图所示图形中是四棱锥三视图的是( )
A、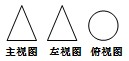 |
B、 |
C、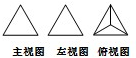 |
D、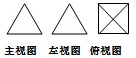 |
 在平面直角坐标系xOy中,已知B(1,0),∠AOB=120°,|
在平面直角坐标系xOy中,已知B(1,0),∠AOB=120°,|