Question

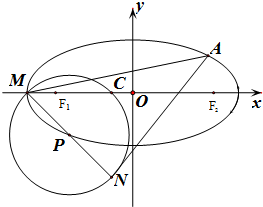已知椭圆E的方程：

x2

a2

+

y2

b2

=1（a＞b＞0），它的两个焦点为F1(-5

3

，0)，F2(5

3

，0)，P为椭圆的一点（点P在第三象限上），且△PF₁F₂的周长为20+10

3

，
（Ⅰ）求椭圆E的方程；
（Ⅱ）求出椭圆的左顶点M的坐标，MP交圆P与另一点N的坐标，若点A在椭圆E上，使得

AM

•

AN

=-32，求点A的坐标．

Answer 1

考点：直线与圆锥曲线的关系,椭圆的标准方程

专题：圆锥曲线的定义、性质与方程

分析：（Ⅰ）直接利用已知条件列出方程组，求出椭圆的几何量，即可求椭圆E的方程；
（Ⅱ）若以点P为圆心的圆过椭圆的左顶点M与点C（-2，0），MP交圆P与另一点N，设A（x，y），通过

AM

•

AN

=-32，求解求点A的坐标．

解答： 解：（Ⅰ）依题意得：|F1F2|=10

3

，又|PF1+PF2|=2a，…（1分）
则有2a+2c=20+10

3

…----…（2分）
∴a=10，b=5，…（4分）
椭圆E的方程：

x2

100

+

y2

25

=1…（5分）
（Ⅱ）由（ 1 ）得M（-10，0），C（-2，0）…（6分）
设点P（m，n），则有m=

-10+(-2)

2

=-6，
又：

m2

100

+

n2

25

=1，∴n=-4，即P（-6，-4），…（8分）
∵P为MN的中点，可得N（-2，-8）…（9分）
设A（x，y），∴

AM

=(-10-x，-y)，

AN

=(-2-x，-8-y)，
∴

AM

•

AN

=(-10-x)(-2-x)+(-y)(-8-y)=x2+12x+20+y2+8y…（10分）
∴

AM

•

AN

=(x+6)2+(y+4)2-32=-32，…（11分）
得x=-6，y=-4时，∴A（-6，-4）…---…（12分）

点评：本题考查椭圆的标准方程的求法，直线与椭圆的位置关系的应用，考查转化思想以及计算能力．