题目内容
 设函数f(x)=x+
设函数f(x)=x+| a |
| |x| |
(1)当x>0时,若f(x)的最小值为2,求正数a的值;
(2)当a=1时,作出函数y=f(x)的图象并写出它的单调增区间(不必证明).
考点:函数的最值及其几何意义,函数图象的作法
专题:函数的性质及应用
分析:(1)当x>0时,根据基本不等式的性质,即可求正数a的值;
(2)当a=1时,做出函数的图象,即可得到结论.
(2)当a=1时,做出函数的图象,即可得到结论.
解答:
解(1)∵a>0,x>0,
则由f(x)=x+
≥2
,
由2
=2得,a=1; (6分)
(2)当a=1时,f(x)=x+
=x+
=
.
作出对应的函数图象如图:
函数f(x)=x+
的单调增区间是(-∞,0)和[1,+∞).

则由f(x)=x+
| a |
| x |
| a |
由2
| a |
(2)当a=1时,f(x)=x+
| a |
| |x| |
| 1 |
| |x| |
|
作出对应的函数图象如图:
函数f(x)=x+
| 1 |
| |x| |
点评:本题主要考查函数最值的应用,利用基本不等式的性质是解决本题的关键.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
已知函数f(x)=x3-3x,若△ABC中,角C是钝角,那么( )
| A、f(sinA)>f(cosB) |
| B、f(sinA)<f(cosB) |
| C、f(sinA)>f(sinB) |
| D、f(sinA)>f(sinB) |
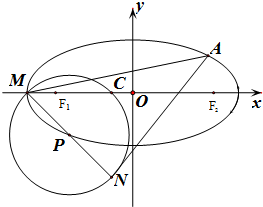 已知椭圆E的方程:
已知椭圆E的方程: